Procedural modeling of Muqarnas: Difference between revisions
| Line 122: | Line 122: | ||
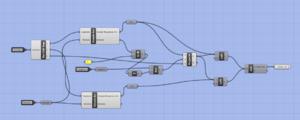
| [[File:cell_circuit.PNG|thumb|The grasshopper circuit for a cell]] | | [[File:cell_circuit.PNG|thumb|The grasshopper circuit for a cell]] | ||
| [[File:cell_square_in_progress.PNG|thumb|Step 1. The Arcs along the Module Segments and the Arc's projection along the diagonal are highlighted.]] [[File:Int_square_progress.PNG|thumb|Step 1.]] [[File:Half_square_cell_progress.PNG|thumb|Step 1.]] | | [[File:cell_square_in_progress.PNG|thumb|Step 1. The Arcs along the Module Segments and the Arc's projection along the diagonal are highlighted.]] [[File:Int_square_progress.PNG|thumb|Step 1.]] [[File:Half_square_cell_progress.PNG|thumb|Step 1.]] | ||
| [[File:cell_square.PNG|thumb|Step 2. The Simple Cell for a square]] | | [[File:cell_square.PNG|thumb|Step 2. The Simple Cell for a square]] [[File:Int_square.PNG|thumb|Step 1.]] [[File:Half_square_cell.PNG|thumb|Step 1.]] | ||
|} | |} | ||
Revision as of 20:26, 21 December 2022
Introduction & Motivation
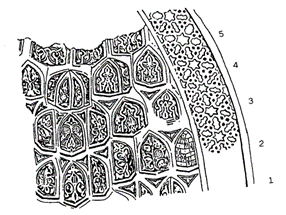
Muqarnas is a type of 3D ornamentation used in Islamic Architecture. This form of ornamentation was first developed during the Abbasid Empire. It is a complex stalactite vaulted structure composed of different units arranged one on top of another and spanning several tiers. The primary purpose of Muqarnas was to create a transition between a circular dome and the square structure beneath it.
This project uses procedural modeling to recreate several types of 3D Muqarnas models based on fixed sets of rules.
The logic followed to recreate 3D muqarnas models is mainly based on the book Miftah al-Hisab, Volume II: Geometry written in 1427 by Jamshid Al Kashi, a 15th century Persian mathematician and astronomer. In this book, Al Kashi tries to simplify complex geometric calculations in a way that lets artisans who do not have a thorough mathematical understanding to efficiently and accurately perform calculations necessary for taking measurements of the structures they are constructing.
The third section of his book On the surface area of the muqarnas contains three key points interesting for our project:
1. Muqarnas Definition
2. Muqarnas elements
3. Muqarnas Types
Muqarnas Definition
In his book, Al Kashi gave the following definition of a Muqarnas:
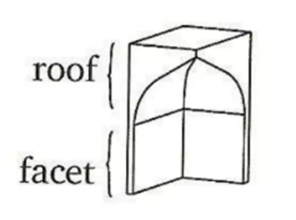
“A muqarnas is a stair-like ceiling that has facets and a surface. Each facet intersects with its adjacent either on a right angle or half a right angle or the sum of one and a half right angles, or others. The two facets can be thought of as perpendicular to a plane parallel to the horizon. Built over these two facets is a plane not parallel to the horizon, or two planes, or two curved surfaces, which are the ceiling of the facets. The two facets along with their ceiling are called a cell. Adjacent cells with bases on the same plane parallel to the horizon are called a tier. The length of the base of the largest facet is called the module of the muqarnas.”
Facet: vertical side of a unit
Roof: plane not parallel to the horizon, or two planes, or two curved surfaces on top of the facets
Cell: two facets along with their roofs
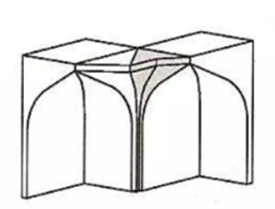
Intermediate element: surface, or two joint surfaces, connecting the roofs of two adjacent cells
Tier: Adjacent cells with bases on the same plane parallel to the horizon
Module: length of the base of the largest facet
Muqarnas elements
Al Kashi describes five types of elements. The two main ones are the square and the rhombus, whose sides are equal to the module defined. Other elements mentioned are the Almond, Biped and Barley-Kernel.
Muqarnas Types
1. Simple Muqarnas: the ceilings have plane surfaces only
2. Clay-plaster muqarnas: simple muqarnas but the tiers do not have the same height
3. Curved muqarnas: surfaces of the ceilings are curved
4. Shirazi-style muqarnas: like curved muqarnas but with a larger variety of elements
Methodology
Create the shapes in 2D
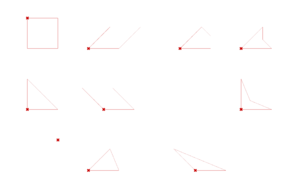
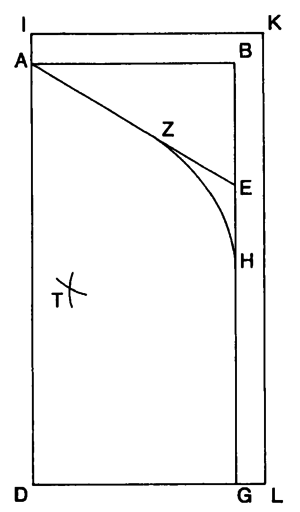
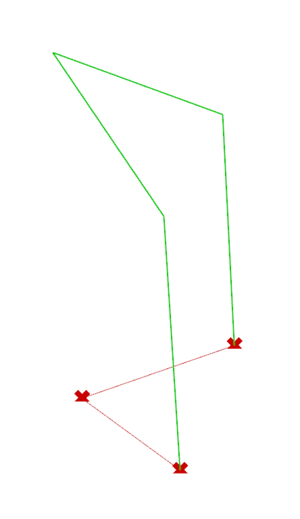
The first elements we constructed on Grasshopper are the base shapes found in the floorplans of muqarnas. Each of these shapes has at least one segment with a length equal to the module: we will call it the Module Segment.
The Dold research paper on Al-Kashi’s book explains the geometrical steps to construct them. However, we also need to parametrize our shape builders – that is, allow them to produce a shape from any set of input points in the XY plane and any module length while still respecting the geometrical rules of construction. To do so, we implement each shape using a three-point system:
- The origin: one vertex of the shape, it always corresponds to one end of the Module Segment. The origin is often the first vertex mentioned in the construction process and from which the other vertices of the shape are built.
- The direction point: a point which determines in which direction from the origin the Module Segment will be built. It does not correspond to any vertex of the shape, unless placed one module away from the origin.
- The symmetry point: this point is placed on either side of the vector created by the origin and the direction point and determines on which side of the Module Segment the rest of the shape will be built. It does not correspond to any vertex of the shape.
Each shape builder takes these three points and the module length as inputs and returns as outputs
- The shape (as a curve),
- A list of its vertices,
- Its diagonal starting from the origin,
- The module.
With this system, we can easily build shapes tessellating next to each other, by connecting one shape’s vertices to another shape builder.
Transform the shapes in 3D
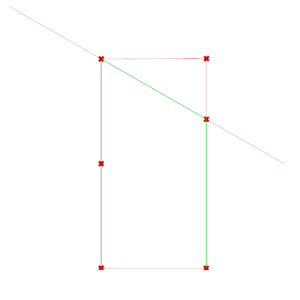
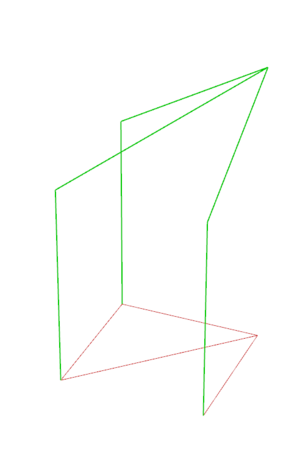
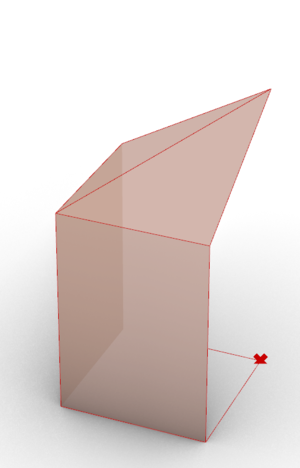
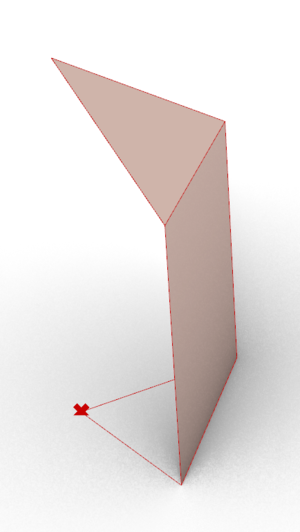
The next step is to obtain the 3D elements from the base shapes. There are 3 types of elements: a cell for a full-shape, an intermediate element, and a cell for a half-shape.
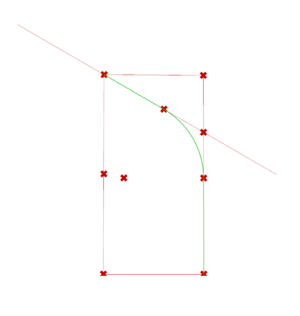
The Arc from the Method of Masons
We build the arc according to which the base shape will be projected in order to form a cell. The construction process of this arc is detailed in the Dold research paper. With the first few steps of the process, we create the Simple Arc.
The rest of the process allows us to create the Curved Arc.
The 3D Projection
Next, this is how we construct a Cell for a full-shape.
- Step 1: we select two adjacent module segments on the shape, and construct instances of the same Arc (simple or curved) along them. These two arcs are positioned such that they start on two different points and end (at their highest point) over the origin of the shape. Then, we project this arc onto the diagonal of the shape.
- Step 2: we simply use a loft on these Arcs in order to create the cell's surface.
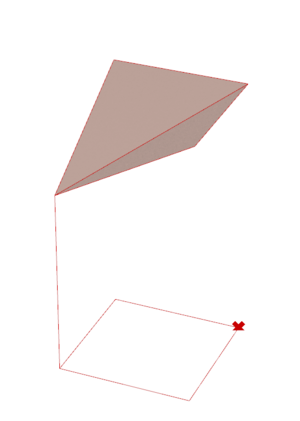
The process to create a cell for a half-shape is the same, except there is no need to project the arc onto a diagonal.
The process to create an intermediate element is also similar to that of the full-shape cell, save for the fact that we select different segments along which to construct the arcs. In the case of an intermediary element, the arcs are positioned to both start from the point opposite to the origin.
Create the 2D plan and the 3D volume
The 2D plan and the 3D volume of the Muqarnas are created in parallel. The same process is used for each layer, with only the base shape and type of 3D element (cell or intermediate) changing.
- Step 1: for the first/top tier, we create three points anywhere on the canvas. One of these will be the highest point of the model, and will be used in every layer's construction: we call it the Super Center.
- Step 2: we select a shape and build it with the help of our three points. We also create its corresponding 3D element, alternating at each layer between a cell and an intermediate element (the top tier is always composed of cells)
- Step 3: we create two polar arrays (one for shapes, one for cells) around the Super Center, so that the elements are adjacent without overlapping.
- Step 4: we move the array of 3D elements along the Z-axis to account for the change in tier.
- Step 5: using the polar array of 2D shapes, we create a curve corresponding to the outer boundary of the 2D plan. Then, using distance calculations, we extract three points from this boundary: these points form an angle A in which we can build the base shape of the next layer.
We repeat steps 2 to 5 for each layer, until we obtain an angle A measuring 180 degrees or more: in this case, there is no shape that can be built in the angle.
In practice
Project Plan
The project is separated in three main goals: identify the historical document to use, develop the procedural modeling methods and perform the modeling. The following table provides the project plan:
| Date | Task | Completion |
|---|---|---|
| By Week 3 |
|
✓ |
| By Week 4 |
|
✓ |
| By Week 5 |
|
✓ |
| By Week 6 |
|
✓ |
| By Week 7 |
|
✓ |
| By Week 8 |
|
✓ |
| By Week 9 |
|
✓ |
| By Week 10 |
|
✓ |
| By Week 11 |
|
✓ |
| By Week 12 |
|
✓ |
| By Week 13 |
|
✓ |
| By Week 14 |
|
✓ |
Results
3D shapes
3D shapes with curve
Simple Muqarnas
Curved Muqarnas
Limitations
Future work
In the future, it would be interesting to have a fully automatic way to generate Muqarnas, where the user would be able to choose the type, a base shape, and the number of tiers as input and would get all the different muqarnas combinations possible as output.
The work could also be extended to cover Clay-plastered and Shirazi style Muqarnas.
Another interesting possibility would be to calculate the surface area of the Muqarnas based on the method that Al Kashi formulates in his book and compare it to the actual surface calculated on Grasshopper.
Github Repository
Procedural Modeling of Muqarnas
References
Literatures
- Al-Kashı-'s Miftah al-Hisab original manuscript: Qatar National Library
- Nuh Aydin, Lakhdar Hammoudi, Ghada Bakbouk, Al-Kashi's Miftah al-Hisab, Volume II: Geometry: Translation and Commentary 1st ed. 2020 Edition, Birkhauser
- Dold‐Samplonius, Yvonne. (2007). Practical Arabic Mathematics: Measuring the Muqarnas by al‐K¯ash¯i. Centaurus. 35. 193 - 242. 10.1111/j.1600-0498.1992.tb00699.x.
- Hamekasi, N. & Samavati, Faramarz & Nasri, Ahmad. (2011). Interactive Modeling of Muqarnas. Proceedings - CAe 2011: International Symposium on Computational Aesthetics in Graphics, Visualization, and Imaging. 129-136. 10.1145/2030441.2030469.