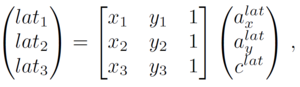Shortest-Path Route Extraction From City Map: Difference between revisions
| (99 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
== Motivation == | |||
The idea of our project is to give people a glimpse of what it was like to navigate through Manhattan in the past, specifically in 1829, at a time when New York City was experiencing rapid growth. To accomplish this, we built a direction-finding tool which was inspired by Google Maps and similar services. This tool allows a user to find the shortest path between start and end points selected on a map. It also computes estimated travel times and takes into account both the layout of the city as it was at the time, and the modes of transportation available at the time. | |||
This gives the interested user the chance to appreciate how navigation was different two centuries ago from what it is like now and to explore how both routes and travel times have evolved. | |||
== The Historical Document == | == The Historical Document == | ||
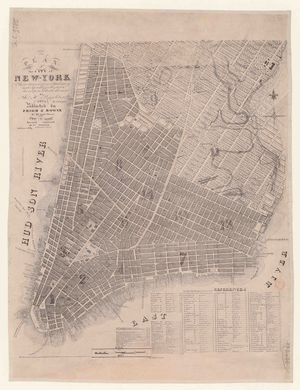
[[File:Manhattan-1829_base-map.jpg|300px|right|thumb|Original map which forms the basis of the project. Note the distinction between already built sections (darker, south-west) and unfinished or planned sections (lighter, north-east).]] | [[File:Manhattan-1829_base-map.jpg|300px|right|thumb|Original map which forms the basis of the project. Note the distinction between already built sections (darker, south-west) and unfinished or planned sections (lighter, north-east).]] | ||
We are working on a historical map of Manhattan, depicting mostly Lower Manhattan as well as some part to the north-east | We are working on a historical map of Manhattan<ref name="basemap" />, depicting mostly Lower Manhattan as well as some part to the north-east side. The following is a compilation of some contextual information retrieved directly from within the map: | ||
* | * Self-designated as "Plan of the City of New-York" | ||
* | * Published in 1829 | ||
* | * In the English language | ||
* | * Source material of the map states: "The greater part from actual survey made expressly for the purpose (the rest from authentic documents)" | ||
* | * By Thomas H. Pappleton, City Surveyor | ||
* | * Published by Prior & Bowne | ||
* | * Revised and corrected by William Hooker | ||
The map features a clear visual distinction between two sections. The first one, delimited to the north-east by North Street, Bowery, | The map features a clear visual distinction between two sections. The first one, delimited to the north-east by North Street, Bowery, Eighth Street, Greenwich Lane, and Great Kill Road, is characterized by buildings drawn shaded-in. This is in contrast to the other section, where buildings are drawn more lightly. Places that are superimposed over roads are drawn in a dashed style. The former section depicts parts of the city that are already built, while the latter represents parts that are unfinished or only at a planning stage. While this interpretation is natural, it is not evident beyond doubt from the map itself (which lacks a legend) what the meaning of the different shadings of the buildings is. However, another map<ref name="map_1836" /> from around the same time (1836), allowed us to draw this conclusion. This other map contains a broadly similar division, as well as a legend revealing the darker areas as "section[s] of city built" and the lighter ones as either "opened or being regulated" or "established by ordinance". | ||
For the project, only the darker section on the map, corresponding to already built parts of the city, is used | For the project, only the darker section on the map, corresponding to already built parts of the city, is used - the rest is ignored. | ||
== Extraction | == Implementation Details == | ||
For the proposed application, the relevant information that needs to be extracted from the map is | === Graph Extraction === | ||
For the proposed application, the relevant information that needs to be extracted from the map is a usable representation of the road network. For this, the Python tool [http://nefi.mpi-inf.mpg.de NEFI]<ref name="NEFI" /> (''Network Extraction From Images''), developed at ''Max Planck Institut für Informatik'', is used. The tool performs automated detection of networks in images based on the Guo-Hall thinning algorithm<ref name="Guo-Hall" /> and outputs the extracted network as an undirected planar graph, stored in a text file. Intersections are the nodes of the graph in this representation, while roads are edges. Besides the fundamental graph extraction step, the tool also provides functionality for some basic image preprocessing before graph extraction, as well as some options for post-processing the extracted graph. | |||
However, simply running NEFI on the map image, as it is, is not enough to get satisfactory graph extraction results. In fact, for the application at hand, nothing less than an optimal graph is acceptable since a graph where edges and nodes do not accurately coincide with roads and intersections will be either unsuitable for direction-finding or at least visually displeasing when overlaying computed routes onto the map image. A desirable workflow for the whole graph extraction process might look like this: | |||
* Crop the image, remove from the outset portions of the image that are irrelevant (in this case: margins, sea, sections corresponding to parts of the city not yet built), basic image preprocessing (e.g. contrast | * Crop the image, remove from the outset portions of the image that are irrelevant (in this case: margins, sea, sections corresponding to parts of the city not yet built), basic image preprocessing (e.g. enhance contrast, blur). While the latter could be achieved using NEFI's inbuilt preprocessing capabilities, these are fairly limited, so using an external program is likely advisable. | ||
* Automated graph extraction using NEFI. | * Automated graph extraction using NEFI. | ||
* Visually assessing and, as required, manually correcting inaccuracies in the graph extracted from the map. For this task, ideally, we would need a GUI tool that provides the possibility to overlay the graph onto the original map and, directly in this view, | * Visually assessing and, as required, manually correcting inaccuracies in the graph extracted from the map. For this task, ideally, we would need a GUI tool that provides the possibility to overlay the graph onto the original map and, directly in this view, permit manual editing of nodes and their connections in accordance with the underlying image. | ||
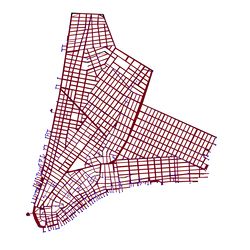
[[File:Manhattan-1829_graph.jpg|250px|right|thumb|Map that was manually segmented into roads (black) and inaccessible areas (white), with the graph extracted overlaid on top. Blue: nodes. Red: edges.]] | |||
Unfortunately, no such convenient way of correcting errors in the extracted graphs by means of a graphical editor was found. This leaves us with no option for correcting graph errors but editing directly the text file in some way, which is highly impractical. As a result, the preprocessing and cleaning of the image before graph extraction becomes all the more important. To get decent results, we had to resort to rather heavy preprocessing, manually segmenting the image into roads and inaccessible areas (i.e., coloring them black and white, respectively) using GIMP<ref name="GIMP" /> (''Gnu Image Manipulation Program''). Graph extraction using NEFI is then run on the manually segmented image. The pipeline that was specified in NEFI consists of the following steps | Unfortunately, no such convenient way of correcting errors in the extracted graphs by means of a graphical editor was found. This leaves us with no option for correcting graph errors but editing directly the text file in some way, which is highly impractical. As a result, the preprocessing and cleaning of the image before graph extraction becomes all the more important. To get decent results, we had to resort to rather heavy preprocessing, manually segmenting the image into roads and inaccessible areas (i.e., coloring them black and white, respectively) using GIMP<ref name="GIMP" /> (''Gnu Image Manipulation Program''). Graph extraction using NEFI is then run on the manually segmented image. The pipeline that was specified in NEFI consists of the following ordered steps: | ||
* "Watershed DE Otsus" from category ''Segmentation'', short for "Watershed with Dilation, Erosion and Otsu’s Threshold". Default settings are used. | * "Watershed DE Otsus" from category ''Segmentation'', short for "Watershed with Dilation, Erosion and Otsu’s Threshold". Default settings are used. | ||
* "Guo Hall Thinning" from category ''Thinning''. This algorithm does not have any settings. | * "Guo Hall Thinning" from category ''Thinning''. This algorithm does not have any settings. | ||
* "Guo Hall Graph Detection" from category ''Graph Detection''. This algorithm does not have any settings. | * "Guo Hall Graph Detection" from category ''Graph Detection''. This algorithm does not have any settings. | ||
* "Keep only LCC" from category ''Graph Filtering''. This removes all but the longest connected | * "Keep only LCC" from category ''Graph Filtering''. This removes all but the longest connected components from the graph obtained. This algorithm does not have any settings. | ||
We realize this approach is far from ideal, and not very efficient, since the manual segmentation in the preprocessing step actually amounts to (implicitly) doing a big part of the graph extraction by hand, but the indirect route via NEFI still has to be taken for the actual graph extraction. We nonetheless decided to stick to that approach, since it works in principle, and spending more time searching for a user-friendly tool for manual extraction and editing of graphs based on images was deemed not worthwhile. However, for future similar projects, it might be advisable to invest some time in researching, or even creating, such a tool. Having such a tool at one's disposal, one could | We realize this approach is far from ideal, and not very efficient, since the manual segmentation in the preprocessing step actually amounts to (implicitly) doing a big part of the graph extraction by hand, but the indirect route via NEFI still has to be taken for the actual graph extraction. We nonetheless decided to stick to that approach, since it works in principle, and spending more time searching for a user-friendly tool for manual extraction and editing of graphs based on images was deemed not worthwhile. However, for future similar projects, it might be advisable to invest some time in researching, or even creating, such a tool. Having such a tool at one's disposal, one could perform manual graph extraction conveniently: forgoing the indirect route via NEFI entirely. Alternatively, you could cut down on the necessary preprocessing before the automated graph extraction via NEFI, since there would now be a feasible way of correcting errors afterwards. | ||
Additionally, the manual segmentation during the preprocessing inevitably introduces some human-input-related ambiguity. However, this is not inherently different from the ambiguity that would arise in direct manual graph extraction or the ambiguity involved with assessing the accuracy of an extracted graph. Some degree of ambiguity of this type therefore seems unavoidable. | |||
=== Relating to Real-World Coordinates and Distances === | |||
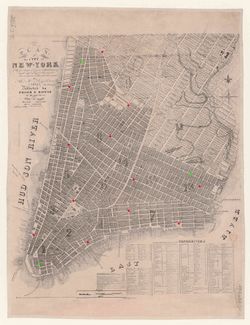
[[File:Manhattan-1829_reference-and-checking-points.jpg|250px|right|thumb|Map with the reference and checking points highlighted that were manually matched to real-world coordinates. Green: The three reference points based on which the conversion parameters were computed. Red: Additional 12 points used for quantifying the inaccuracy of that conversion.]] | |||
The output we get from NEFI, as detailed in the [[Shortest-Path_Route_Extraction_From_City_Map#Graph_extraction|previous section]], is a planar representation of the road network, where the coordinates of nodes correspond to pixel coordinates in the image from which the graph was extracted. A priori, this is not meaningful. To make those coordinates meaningful, we need to link them to real-world coordinates and distances. | |||
We briefly explored the idea of using georeferencing by means of the software QGIS<ref name="QGIS" /> to help us with this. However, we could not find any information on the reference ellipsoid and projection system used in the historical map, which is information required for geo-referencing. Additionally, we encountered what we believe is a bug in QGIS (but might also be merely incorrect usage) where raster maps above a certain size (pixel number, not file size) are not displayed correctly in the program. We therefore abandoned this idea. | |||
Instead, we decided to approximately solve these problems by assuming a linear transformation between graph and real-world coordinates (i.e. disregarding all curvature effects) and explicitly working out by ourselves the conversion factors involved. Later, we will [[Shortest-Path_Route_Extraction_From_City_Map#Conversion_errors|give an estimate of the error caused by this linearization]]. The first step in this process is to find three reference intersections, that are clearly identifiable both on the historical map and on a modern map. For these three reference intersections, the coordinates of the corresponding nodes on the graph, and their real-world latitude and longitude (read manually from Google Maps) are registered. | |||
For converting the coordinates of graph nodes to real-world latitude and longitude, we assumed the linear relations | |||
[[File:formula_graph-to-lat.png|240px|center|]] | |||
[[File:formula_graph-to-long.png|280px|center|]] | |||
with coefficients ''a<sub>x</sub><sup>lat</sup>, a<sub>y</sub><sup>lat</sup>, c<sup>lat</sup>, a<sub>x</sub><sup>long</sup>, a<sub>y</sub><sup>long</sup>, c<sup>long</sup>'' to be determined. To that end, we solved the system of linear equations (shown only for latitudes, but it works anaologously for longitudes) | |||
[[File:formula_system-of-equations.png|300px|center|]] | |||
where (''x<sub>i</sub>, y<sub>i</sub>''), ''i''=1,2,3, are the graph coordinates of the three reference intersections and ''lat<sub>i</sub>'' are their latitudes in degrees. | |||
For calculating the real-world distance between two points in the graph coordinate system, we employ the first-order approximation | |||
[[File:formula_distance-graph-to-real.png|180px|center|]] | |||
where ''d<sub>real</sub>'' is the real-world distance along geodesics, ''d<sub>graph</sub>'' is the 2-norm of the difference between two points in the graph coordinate system, and alpha is a uniform scale factor between them. To find the scale factor, we are then simply taking the ratio ''d<sub>real</sub>/d<sub>graph</sub>''. In principle, it is sufficient to do this for only one reference distance. However, we did it for all three sides of the triangle formed by the three reference intersections, followed by taking the mean, to make the result less susceptible to possible inaccuracies in identifying the matching points between the historic and modern map. To compute the real-world distances ''d<sub>real</sub>'', we used Wolfram Mathematica's GeoDistance function<ref name="GeoDistance" />, which takes curvature effects into account. | |||
While the conversion from graph coordinates to latitude/longitude and the conversion from graph distances to real-world distances are based on the same three reference points, the two conversions are otherwise independent and do not make use of each other. The conversion to latitude and longitude is in fact only used for displaying positions when hovering over the map with the cursor, and for displaying coordinates of destinations in the sidebar on the webpage. | |||
=== Website Implementation === | |||
We created a [http://www.dhproject.cf/ website] to showcase our project. The website contains the NEFI text file that contains node and edge coordinates and is outputted during graph extraction. From here, everything is dynamically generated in the browser using Javascript. There are three main components that work towards displaying the final product: | |||
* Graph Parsing: We start by iterating through each line of the NEFI output file. This allows us to construct an edge-list and node-list representation of our graph. These edge and node lists are later used to build an interactive graph object. We also store a list of paths, which is a combination of nodes and edges together. This path list allows us to compute shortest paths later. | |||
* Shortest-Path Routing: We use Dijsktra’s Algorithm<ref name="Dijkstra" /> to determine shortest routes between intersections. We wrote a custom implementation of the algorithm that runs in the browser whenever a user creates a new route. We decided to compute the paths in the browser (rather then precompute and send the information to the user in a file) in the interest of fast load times for the user. Dijkstra’s algorithm runs quite fast and has a minimal performance impact in the browser. We also compute the travel times for pedestrians<ref name="pedestrian-speed" /> and horses<ref name="horse-speeds" /> in parallel with Dijkstra. | |||
* Interactive Graph Drawing: We use Plotly<ref name="Plotly" /> to display an interactive map to the user. At its core, the map overlays an invisible planar graph onto the image of the old map. We found that we needed to do light manipulation of the dimensions of the planar graph to perfectly align it with the map image. | |||
== Quantitative Analysis of Extraction Performance == | |||
=== Graph Extraction Performance === | |||
Quantifying the quality of the graph extraction proved challenging. The difficulty is in fact twofold. | |||
* Firstly, the quality of the automatic graph extraction performed by NEFI should be estimated. That is to say, a measure of how close the graph returned by the extraction alogrithm is to the "true" underlying graph should be computed and reported. However, developing or computing such a measure of closeness between graphs is not an easy task <ref name="on-graph-extraction-from-image-data" /> and we finally had to settle for simply stating that, upon visual inspection of the graph output compared to the original image, we did not notice any errors that cause the road network to be significantly misreprented. That being said, some slight imperfections could be observed due to the fact that NEFI cannot detect nodes of degree 2 (nodes from which exactly two edges originate), and instead straightens the two originating nodes into a single long one. This is an inherent limitation of the algorithm used, which is also acknowledged by the authors of the program<ref name="NEFI_nodes-degree-2" />. These types of nodes correspond to bends or curves in roads rather than intersections between roads, and therefore are not actually relevant to the topology of the network. Nonetheless, the fact that they are not correctly recognized can be unaesthaetic in the visualization of paths, and means that some distance calculations might be slightly off. | |||
* Secondly, even if such a metric for judging the similarity between an extracted graph and a "true" graph was easily available, the ground truths to compare the extracted graph to are themselves far from unambiguous. This is because intersections are objects with a finite spatial extent, and it might therefore not always be certain where the corresponding node, which is just a point with a single definite position, is to be placed. Furthermore, in the case of larger accessible areas on the map (large intersections, squares or parks) it is in fact not even certain for a human how many nodes should be placed in that area. Finally, there might be places on the map with uncertain interpretation as to whether an area is to be considered accessible or inaccessible. So, overall, we were forced to take some liberties in defining what the "correct" graph representation of the road network should look like. As opposed to the problem of checking automated graph extraction described above, this is an inherent problem that is also present when the graph extraction is done fully by hand with no automation whatsoever. In our project, even though we are not explicitly performing any manual graph extraction, the manual segmentation of the image in the preprocessing step also amounts to making a decision on what the graph should look like and consequently carries the same problem. This manual segmentation was done by one team member alone. Therefore, to estimate the variability in the baseline graph due to different people interpreting the map differently, we selected a small region of the map, and both of us counted the number of nodes they believed they could clearly identify in that region, as well as the number of spots where we were uncertain how many nodes should be placed there. Finally, we compared those numbers. Doing so, we got 133 nodes and 7 uncertain regions versus 147 nodes and 4 uncertain regions. This reflects different opinions on what constitutes a single node, but there were no disagreements on the large-scale topology of the network in that region. While doing this counting on only a subset of the entire map clearly gives a biased result, we expect the result to generalize favorably to the whole map (i.e. there to be relatively less disagreement between people when considering the entire map), since the selected region is one of the most irregular and therefore not so easy to interpret. | |||
=== Linearization Errors === | |||
To quantify the errors incurred by linearizing the dependence of latitudes/longitudes and real-world distances on the graph coordinates, we selected another twelve matching points on the historic and modern map (Google Maps), and noted their graph node coordinates and corresponding real-world latitude/longitude. This is on top of the three reference points already selected for computing the conversion parameters. | |||
We tried to select those twelve points used for checking in such a way that they are more or less evenly distributed across the map. However, we did not have total liberty to do so, since not all features visible on the historical map are still present in modern-day New York: which forced us to slightly restrict our choice. | |||
The following table shows the real latitudes and longitudes of the twelve points, and the errors of the computed latitudes and longitudes with respect to real-world ones. We find that the maximum error (by absolute value) is 0.000274527° for the latitudes and 0.000342848° for the longitudes. | |||
{| class="wikitable" | |||
! number of checking point | |||
! lat<sub>real</sub> [degrees] | |||
! long<sub>real</sub> [degrees] | |||
! lat<sub>computed</sub> - lat<sub>real</sub> [degrees] | |||
! long<sub>computed</sub> - long<sub>real</sub> [degrees] | |||
|- | |||
|1 ||40.714186 ||-74.006306 ||-0.000189 ||-0.000275 | |||
|- | |||
|2 ||40.711329 ||-73.983644 ||-0.000074 ||-0.000343 | |||
|- | |||
|3 ||40.718167 ||-73.993845 ||-0.000103 ||-0.000251 | |||
|- | |||
|4 ||40.717533 ||-73.980001 ||-0.000009 ||-0.000032 | |||
|- | |||
|5 ||40.708233 ||-74.014393 ||-0.000279 ||-0.000245 | |||
|- | |||
|6 ||40.707226 ||-74.002751 ||0.000101 ||-0.000256 | |||
|- | |||
|7 ||40.723291 ||-74.008029 ||-0.000165 ||-0.000251 | |||
|- | |||
|8 ||40.730166 ||-73.996082 ||0.000082 ||-0.000016 | |||
|- | |||
|9 ||40.732668 ||-74.008626 ||-0.000076 ||-0.000230 | |||
|- | |||
|10 ||40.738769 ||-74.002449 ||0.000041 ||0.000171 | |||
|- | |||
|11 ||40.725006 ||-73.999357 ||-0.000082 ||-0.000213 | |||
|- | |||
|12 ||40.713022 ||-73.994455 ||-0.000137 ||-0.000256 | |||
|} | |||
Next, we turned our attention to the errors in the distance calculations. Ideally, we would compare the lenghts of shortest-paths under the constraints of the road network, computed by our application and by Google Maps (or a similar tool). Unfortunately, due to the changes to the city over time, the paths will simply not be the same and no such comparison can be made. We will therefore only compare straight-line distances. From the twelve control points chosen, 66 unordered pairs of points can be formed. For these 66 pairs, we calculated the real-world straight-line distances ''d<sub>real</sub>'' (using Wolfram Mathematica's GeoDistance function<ref name="GeoDistance" />) and the straight-line distances ''d<sub>computed</sub>'' that our approximative method gives us, and then calculated the errors ''d<sub>computed</sub>'' - ''d<sub>real</sub>''. The maximum error (by absolute value) found among the 66 pairs of points was 67.402 meters. | |||
To put this into perspective, if we assume that the typical extent of an intersections is between 10 and 20 meters along both directions, then we can note that the linearization error is at least on the same order of magnitude. | |||
The following figures visualize the distribution of the distance errors found as a function of the real distances between points. | |||
{| class="wikitable" width=100% | |||
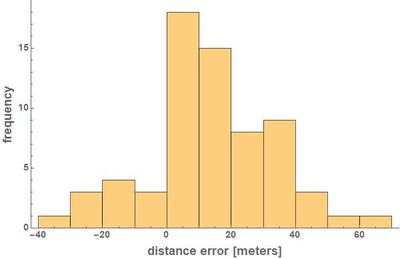
|[[File:distance-errors_histogram.jpg|400px|center|thumb|Histogram showing the frequency distribution of different values of the distance error, for all 66 points of pairs analyzed. Note how there is bias towards positive distance errors, i.e, our compuation method tends to overestimate the real-world distance more often than underestimate it.]] | |||
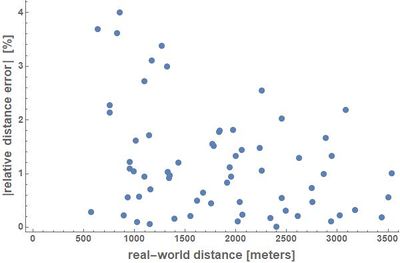
|[[File:relative-distance-errors_plot.jpg|400px|center|thumb|Absolute values of relative distance errors ''err<sub>relative</sub>''=(''d<sub>computed</sub>'' - ''d<sub>real</sub>'')/''d<sub>real</sub>'', expressed as percentages, plotted over the real-world distances for all 66 points of pairs. The largest relative distance errors are in fact observed at the lower end of the distance range. This might be due to the fact that the scale factor relating graph and real-world distances was computed for pairs that are rather far apart.]] | |||
|- | |||
|} | |||
== Project Plan and Milestones == | == Project Plan and Milestones == | ||
| Line 35: | Line 140: | ||
Note that, by design, this section is a snapshot of the project planning at an intermediary stage (as of November 14), and therefore might not accurately reflect all steps taken at later stages. | Note that, by design, this section is a snapshot of the project planning at an intermediary stage (as of November 14), and therefore might not accurately reflect all steps taken at later stages. | ||
Our final goal is to create a simple Google-Maps-style navigation tool for the past. The user will be able to select two points, and see the shortest path between these two points. This would be | Our final goal is to create a simple Google-Maps-style navigation tool for the past. The user will be able to select two points, and see the shortest path between these two points. This would be useful for someone to estimate how they would navigate through a city - possibly hundreds of years ago. Florian has been tasked with pre-processing the historical map. This involves searching for the best maps and cleaning them. Cleaning is crucial to ensure that an accurate graph is extracted from the map. Jonathan is working on representing the graph visually, creating interactivity, and hosting it on a website. | ||
=== Already Completed === | === Already Completed === | ||
| Line 72: | Line 177: | ||
* (Stretch goal) Allow a user to upload their own map which will be processed and displayed. | * (Stretch goal) Allow a user to upload their own map which will be processed and displayed. | ||
== Links == | |||
* [http://www.dhproject.cf/ Project website] | |||
* [https://github.com/jondonas/DH-405/ Github repository] | |||
== References == | == References == | ||
<references> | <references> | ||
<ref name="map_1836">https://www.loc.gov/item/2007627512/</ref> | <ref name="basemap">https://gallica.bnf.fr/ark:/12148/btv1b53099722g/f1.item.r=city, last accessed on 2018-12-05</ref> | ||
<ref name="map_1836">https://www.loc.gov/item/2007627512/, last accessed on 2018-11-30</ref> | |||
<ref name="NEFI">Dirnberger, M. and Kehl, T. and Neumann, A., "NEFI: Network Extraction From Images", ''Scientific Reports'', 5 (2015), http://dx.doi.org/10.1038/srep15669 </ref> | <ref name="NEFI">Dirnberger, M. and Kehl, T. and Neumann, A., "NEFI: Network Extraction From Images", ''Scientific Reports'', 5 (2015), http://dx.doi.org/10.1038/srep15669 </ref> | ||
<ref name="Guo-Hall">Guo, Zicheng & W. Hall, Richard. "Parallel thinning with two-subiteration algorithms". ''Communications of the ACM'' 32 (1989), 359-373. http://doi.acm.org/10.1145/62065.62074</ref> | <ref name="Guo-Hall">Guo, Zicheng & W. Hall, Richard. "Parallel thinning with two-subiteration algorithms". ''Communications of the ACM'' 32 (1989), 359-373. http://doi.acm.org/10.1145/62065.62074</ref> | ||
<ref name="GIMP">https://www.gimp.org/</ref> | <ref name="GIMP">https://www.gimp.org/</ref> | ||
<ref name="QGIS">https://www.qgis.org/en/site/, last accessed on 2018-12-13</ref> | |||
<ref name="GeoDistance">https://reference.wolfram.com/language/ref/GeoDistance.html, last accessed on 2018-12-10</ref> | |||
<ref name="horse-speeds">Harris, Susan E., "Horse Gaits, Balance and Movement", Turner Publishing Company, 2016</ref> | |||
<ref name="pedestrian-speed">Aspelin, Karen, "Establishing Pedestrian Walking Speeds", 2005, https://www.westernite.org/datacollectionfund/2005/psu_ped_summary.pdf</ref> | |||
<ref name="Dijkstra">Dijkstra, E. W., "A note on two problems in connexion with graphs", ''Numerische Mathematik'' 1, 1959, pages 269-271, https://doi.org/10.1007/BF01386390</ref> | |||
<ref name="Plotly">https://en.wikipedia.org/wiki/Plotly</ref> | |||
<ref name="on-graph-extraction-from-image-data">Holzinger, Andreas and Malle, Bernd and Giuliani, Nicola, "On Graph Extraction from Image Data", ''Brain Informatics and Health'' 2014, 552-563, Springer International Publishing</ref> | |||
<ref name="NEFI_nodes-degree-2">https://nefi.mpi-inf.mpg.de/guide.php#limitations, last accessed 2018-12-14</ref> | |||
</references> | </references> | ||
Latest revision as of 10:28, 14 December 2018
Motivation
The idea of our project is to give people a glimpse of what it was like to navigate through Manhattan in the past, specifically in 1829, at a time when New York City was experiencing rapid growth. To accomplish this, we built a direction-finding tool which was inspired by Google Maps and similar services. This tool allows a user to find the shortest path between start and end points selected on a map. It also computes estimated travel times and takes into account both the layout of the city as it was at the time, and the modes of transportation available at the time.
This gives the interested user the chance to appreciate how navigation was different two centuries ago from what it is like now and to explore how both routes and travel times have evolved.
The Historical Document
We are working on a historical map of Manhattan[1], depicting mostly Lower Manhattan as well as some part to the north-east side. The following is a compilation of some contextual information retrieved directly from within the map:
- Self-designated as "Plan of the City of New-York"
- Published in 1829
- In the English language
- Source material of the map states: "The greater part from actual survey made expressly for the purpose (the rest from authentic documents)"
- By Thomas H. Pappleton, City Surveyor
- Published by Prior & Bowne
- Revised and corrected by William Hooker
The map features a clear visual distinction between two sections. The first one, delimited to the north-east by North Street, Bowery, Eighth Street, Greenwich Lane, and Great Kill Road, is characterized by buildings drawn shaded-in. This is in contrast to the other section, where buildings are drawn more lightly. Places that are superimposed over roads are drawn in a dashed style. The former section depicts parts of the city that are already built, while the latter represents parts that are unfinished or only at a planning stage. While this interpretation is natural, it is not evident beyond doubt from the map itself (which lacks a legend) what the meaning of the different shadings of the buildings is. However, another map[2] from around the same time (1836), allowed us to draw this conclusion. This other map contains a broadly similar division, as well as a legend revealing the darker areas as "section[s] of city built" and the lighter ones as either "opened or being regulated" or "established by ordinance".
For the project, only the darker section on the map, corresponding to already built parts of the city, is used - the rest is ignored.
Implementation Details
Graph Extraction
For the proposed application, the relevant information that needs to be extracted from the map is a usable representation of the road network. For this, the Python tool NEFI[3] (Network Extraction From Images), developed at Max Planck Institut für Informatik, is used. The tool performs automated detection of networks in images based on the Guo-Hall thinning algorithm[4] and outputs the extracted network as an undirected planar graph, stored in a text file. Intersections are the nodes of the graph in this representation, while roads are edges. Besides the fundamental graph extraction step, the tool also provides functionality for some basic image preprocessing before graph extraction, as well as some options for post-processing the extracted graph.
However, simply running NEFI on the map image, as it is, is not enough to get satisfactory graph extraction results. In fact, for the application at hand, nothing less than an optimal graph is acceptable since a graph where edges and nodes do not accurately coincide with roads and intersections will be either unsuitable for direction-finding or at least visually displeasing when overlaying computed routes onto the map image. A desirable workflow for the whole graph extraction process might look like this:
- Crop the image, remove from the outset portions of the image that are irrelevant (in this case: margins, sea, sections corresponding to parts of the city not yet built), basic image preprocessing (e.g. enhance contrast, blur). While the latter could be achieved using NEFI's inbuilt preprocessing capabilities, these are fairly limited, so using an external program is likely advisable.
- Automated graph extraction using NEFI.
- Visually assessing and, as required, manually correcting inaccuracies in the graph extracted from the map. For this task, ideally, we would need a GUI tool that provides the possibility to overlay the graph onto the original map and, directly in this view, permit manual editing of nodes and their connections in accordance with the underlying image.
Unfortunately, no such convenient way of correcting errors in the extracted graphs by means of a graphical editor was found. This leaves us with no option for correcting graph errors but editing directly the text file in some way, which is highly impractical. As a result, the preprocessing and cleaning of the image before graph extraction becomes all the more important. To get decent results, we had to resort to rather heavy preprocessing, manually segmenting the image into roads and inaccessible areas (i.e., coloring them black and white, respectively) using GIMP[5] (Gnu Image Manipulation Program). Graph extraction using NEFI is then run on the manually segmented image. The pipeline that was specified in NEFI consists of the following ordered steps:
- "Watershed DE Otsus" from category Segmentation, short for "Watershed with Dilation, Erosion and Otsu’s Threshold". Default settings are used.
- "Guo Hall Thinning" from category Thinning. This algorithm does not have any settings.
- "Guo Hall Graph Detection" from category Graph Detection. This algorithm does not have any settings.
- "Keep only LCC" from category Graph Filtering. This removes all but the longest connected components from the graph obtained. This algorithm does not have any settings.
We realize this approach is far from ideal, and not very efficient, since the manual segmentation in the preprocessing step actually amounts to (implicitly) doing a big part of the graph extraction by hand, but the indirect route via NEFI still has to be taken for the actual graph extraction. We nonetheless decided to stick to that approach, since it works in principle, and spending more time searching for a user-friendly tool for manual extraction and editing of graphs based on images was deemed not worthwhile. However, for future similar projects, it might be advisable to invest some time in researching, or even creating, such a tool. Having such a tool at one's disposal, one could perform manual graph extraction conveniently: forgoing the indirect route via NEFI entirely. Alternatively, you could cut down on the necessary preprocessing before the automated graph extraction via NEFI, since there would now be a feasible way of correcting errors afterwards.
Additionally, the manual segmentation during the preprocessing inevitably introduces some human-input-related ambiguity. However, this is not inherently different from the ambiguity that would arise in direct manual graph extraction or the ambiguity involved with assessing the accuracy of an extracted graph. Some degree of ambiguity of this type therefore seems unavoidable.
Relating to Real-World Coordinates and Distances
The output we get from NEFI, as detailed in the previous section, is a planar representation of the road network, where the coordinates of nodes correspond to pixel coordinates in the image from which the graph was extracted. A priori, this is not meaningful. To make those coordinates meaningful, we need to link them to real-world coordinates and distances.
We briefly explored the idea of using georeferencing by means of the software QGIS[6] to help us with this. However, we could not find any information on the reference ellipsoid and projection system used in the historical map, which is information required for geo-referencing. Additionally, we encountered what we believe is a bug in QGIS (but might also be merely incorrect usage) where raster maps above a certain size (pixel number, not file size) are not displayed correctly in the program. We therefore abandoned this idea.
Instead, we decided to approximately solve these problems by assuming a linear transformation between graph and real-world coordinates (i.e. disregarding all curvature effects) and explicitly working out by ourselves the conversion factors involved. Later, we will give an estimate of the error caused by this linearization. The first step in this process is to find three reference intersections, that are clearly identifiable both on the historical map and on a modern map. For these three reference intersections, the coordinates of the corresponding nodes on the graph, and their real-world latitude and longitude (read manually from Google Maps) are registered.
For converting the coordinates of graph nodes to real-world latitude and longitude, we assumed the linear relations
with coefficients axlat, aylat, clat, axlong, aylong, clong to be determined. To that end, we solved the system of linear equations (shown only for latitudes, but it works anaologously for longitudes)
where (xi, yi), i=1,2,3, are the graph coordinates of the three reference intersections and lati are their latitudes in degrees.
For calculating the real-world distance between two points in the graph coordinate system, we employ the first-order approximation
where dreal is the real-world distance along geodesics, dgraph is the 2-norm of the difference between two points in the graph coordinate system, and alpha is a uniform scale factor between them. To find the scale factor, we are then simply taking the ratio dreal/dgraph. In principle, it is sufficient to do this for only one reference distance. However, we did it for all three sides of the triangle formed by the three reference intersections, followed by taking the mean, to make the result less susceptible to possible inaccuracies in identifying the matching points between the historic and modern map. To compute the real-world distances dreal, we used Wolfram Mathematica's GeoDistance function[7], which takes curvature effects into account.
While the conversion from graph coordinates to latitude/longitude and the conversion from graph distances to real-world distances are based on the same three reference points, the two conversions are otherwise independent and do not make use of each other. The conversion to latitude and longitude is in fact only used for displaying positions when hovering over the map with the cursor, and for displaying coordinates of destinations in the sidebar on the webpage.
Website Implementation
We created a website to showcase our project. The website contains the NEFI text file that contains node and edge coordinates and is outputted during graph extraction. From here, everything is dynamically generated in the browser using Javascript. There are three main components that work towards displaying the final product:
- Graph Parsing: We start by iterating through each line of the NEFI output file. This allows us to construct an edge-list and node-list representation of our graph. These edge and node lists are later used to build an interactive graph object. We also store a list of paths, which is a combination of nodes and edges together. This path list allows us to compute shortest paths later.
- Shortest-Path Routing: We use Dijsktra’s Algorithm[8] to determine shortest routes between intersections. We wrote a custom implementation of the algorithm that runs in the browser whenever a user creates a new route. We decided to compute the paths in the browser (rather then precompute and send the information to the user in a file) in the interest of fast load times for the user. Dijkstra’s algorithm runs quite fast and has a minimal performance impact in the browser. We also compute the travel times for pedestrians[9] and horses[10] in parallel with Dijkstra.
- Interactive Graph Drawing: We use Plotly[11] to display an interactive map to the user. At its core, the map overlays an invisible planar graph onto the image of the old map. We found that we needed to do light manipulation of the dimensions of the planar graph to perfectly align it with the map image.
Quantitative Analysis of Extraction Performance
Graph Extraction Performance
Quantifying the quality of the graph extraction proved challenging. The difficulty is in fact twofold.
- Firstly, the quality of the automatic graph extraction performed by NEFI should be estimated. That is to say, a measure of how close the graph returned by the extraction alogrithm is to the "true" underlying graph should be computed and reported. However, developing or computing such a measure of closeness between graphs is not an easy task [12] and we finally had to settle for simply stating that, upon visual inspection of the graph output compared to the original image, we did not notice any errors that cause the road network to be significantly misreprented. That being said, some slight imperfections could be observed due to the fact that NEFI cannot detect nodes of degree 2 (nodes from which exactly two edges originate), and instead straightens the two originating nodes into a single long one. This is an inherent limitation of the algorithm used, which is also acknowledged by the authors of the program[13]. These types of nodes correspond to bends or curves in roads rather than intersections between roads, and therefore are not actually relevant to the topology of the network. Nonetheless, the fact that they are not correctly recognized can be unaesthaetic in the visualization of paths, and means that some distance calculations might be slightly off.
- Secondly, even if such a metric for judging the similarity between an extracted graph and a "true" graph was easily available, the ground truths to compare the extracted graph to are themselves far from unambiguous. This is because intersections are objects with a finite spatial extent, and it might therefore not always be certain where the corresponding node, which is just a point with a single definite position, is to be placed. Furthermore, in the case of larger accessible areas on the map (large intersections, squares or parks) it is in fact not even certain for a human how many nodes should be placed in that area. Finally, there might be places on the map with uncertain interpretation as to whether an area is to be considered accessible or inaccessible. So, overall, we were forced to take some liberties in defining what the "correct" graph representation of the road network should look like. As opposed to the problem of checking automated graph extraction described above, this is an inherent problem that is also present when the graph extraction is done fully by hand with no automation whatsoever. In our project, even though we are not explicitly performing any manual graph extraction, the manual segmentation of the image in the preprocessing step also amounts to making a decision on what the graph should look like and consequently carries the same problem. This manual segmentation was done by one team member alone. Therefore, to estimate the variability in the baseline graph due to different people interpreting the map differently, we selected a small region of the map, and both of us counted the number of nodes they believed they could clearly identify in that region, as well as the number of spots where we were uncertain how many nodes should be placed there. Finally, we compared those numbers. Doing so, we got 133 nodes and 7 uncertain regions versus 147 nodes and 4 uncertain regions. This reflects different opinions on what constitutes a single node, but there were no disagreements on the large-scale topology of the network in that region. While doing this counting on only a subset of the entire map clearly gives a biased result, we expect the result to generalize favorably to the whole map (i.e. there to be relatively less disagreement between people when considering the entire map), since the selected region is one of the most irregular and therefore not so easy to interpret.
Linearization Errors
To quantify the errors incurred by linearizing the dependence of latitudes/longitudes and real-world distances on the graph coordinates, we selected another twelve matching points on the historic and modern map (Google Maps), and noted their graph node coordinates and corresponding real-world latitude/longitude. This is on top of the three reference points already selected for computing the conversion parameters. We tried to select those twelve points used for checking in such a way that they are more or less evenly distributed across the map. However, we did not have total liberty to do so, since not all features visible on the historical map are still present in modern-day New York: which forced us to slightly restrict our choice.
The following table shows the real latitudes and longitudes of the twelve points, and the errors of the computed latitudes and longitudes with respect to real-world ones. We find that the maximum error (by absolute value) is 0.000274527° for the latitudes and 0.000342848° for the longitudes.
| number of checking point | latreal [degrees] | longreal [degrees] | latcomputed - latreal [degrees] | longcomputed - longreal [degrees] |
|---|---|---|---|---|
| 1 | 40.714186 | -74.006306 | -0.000189 | -0.000275 |
| 2 | 40.711329 | -73.983644 | -0.000074 | -0.000343 |
| 3 | 40.718167 | -73.993845 | -0.000103 | -0.000251 |
| 4 | 40.717533 | -73.980001 | -0.000009 | -0.000032 |
| 5 | 40.708233 | -74.014393 | -0.000279 | -0.000245 |
| 6 | 40.707226 | -74.002751 | 0.000101 | -0.000256 |
| 7 | 40.723291 | -74.008029 | -0.000165 | -0.000251 |
| 8 | 40.730166 | -73.996082 | 0.000082 | -0.000016 |
| 9 | 40.732668 | -74.008626 | -0.000076 | -0.000230 |
| 10 | 40.738769 | -74.002449 | 0.000041 | 0.000171 |
| 11 | 40.725006 | -73.999357 | -0.000082 | -0.000213 |
| 12 | 40.713022 | -73.994455 | -0.000137 | -0.000256 |
Next, we turned our attention to the errors in the distance calculations. Ideally, we would compare the lenghts of shortest-paths under the constraints of the road network, computed by our application and by Google Maps (or a similar tool). Unfortunately, due to the changes to the city over time, the paths will simply not be the same and no such comparison can be made. We will therefore only compare straight-line distances. From the twelve control points chosen, 66 unordered pairs of points can be formed. For these 66 pairs, we calculated the real-world straight-line distances dreal (using Wolfram Mathematica's GeoDistance function[7]) and the straight-line distances dcomputed that our approximative method gives us, and then calculated the errors dcomputed - dreal. The maximum error (by absolute value) found among the 66 pairs of points was 67.402 meters. To put this into perspective, if we assume that the typical extent of an intersections is between 10 and 20 meters along both directions, then we can note that the linearization error is at least on the same order of magnitude. The following figures visualize the distribution of the distance errors found as a function of the real distances between points.
Project Plan and Milestones
Note that, by design, this section is a snapshot of the project planning at an intermediary stage (as of November 14), and therefore might not accurately reflect all steps taken at later stages.
Our final goal is to create a simple Google-Maps-style navigation tool for the past. The user will be able to select two points, and see the shortest path between these two points. This would be useful for someone to estimate how they would navigate through a city - possibly hundreds of years ago. Florian has been tasked with pre-processing the historical map. This involves searching for the best maps and cleaning them. Cleaning is crucial to ensure that an accurate graph is extracted from the map. Jonathan is working on representing the graph visually, creating interactivity, and hosting it on a website.
Already Completed
- Took the first steps to developing a cleaning process for each map
- Written Python code to display a graph from a text list of nodes and edges
- Completed simple routing between two nodes
- Setup a website and domain (www.dhproject.cf) to showcase our project
Future Goals
- Take a decision on which overall direction to pursue for the remainder of the project: Generality, by including several other maps? Or, adding selection of start and end point based on address input, to more closely mimic the interface and functionality of services like Google Maps? (November 23)
- Letting a user select two nodes on the map, and displaying the shortest path between the two nodes. (November 23)
- Displaying the interactive graph on the website. (November 23)
- Calculating and displaying the actual estimated distance between the two points. (end of November)
- Overlay the graph representation onto the historical map. (end of November)
- Develop a manual process for assessing how accurate graph extraction is, and correcting if necessary. (end of November)
- Some buffer time, to allow for unforeseen work. (December 1 to 9)
- Finish Wiki writing (December 12)
- Refine (and automate) the cleaning process. This may involve researching other maps and choosing the best ones for our needs. (no hard time frame, depending on feasibility and necessity)
- Possibly move the network extraction, which is currently done via GUI, to a script. (no hard time frame, depending on feasibility and necessity)
- (Stretch goal) Allow a user to upload their own map which will be processed and displayed.
Links
References
- ↑ https://gallica.bnf.fr/ark:/12148/btv1b53099722g/f1.item.r=city, last accessed on 2018-12-05
- ↑ https://www.loc.gov/item/2007627512/, last accessed on 2018-11-30
- ↑ 3.0 3.1 Dirnberger, M. and Kehl, T. and Neumann, A., "NEFI: Network Extraction From Images", Scientific Reports, 5 (2015), http://dx.doi.org/10.1038/srep15669
- ↑ Guo, Zicheng & W. Hall, Richard. "Parallel thinning with two-subiteration algorithms". Communications of the ACM 32 (1989), 359-373. http://doi.acm.org/10.1145/62065.62074
- ↑ https://www.gimp.org/
- ↑ https://www.qgis.org/en/site/, last accessed on 2018-12-13
- ↑ 7.0 7.1 https://reference.wolfram.com/language/ref/GeoDistance.html, last accessed on 2018-12-10
- ↑ Dijkstra, E. W., "A note on two problems in connexion with graphs", Numerische Mathematik 1, 1959, pages 269-271, https://doi.org/10.1007/BF01386390
- ↑ Aspelin, Karen, "Establishing Pedestrian Walking Speeds", 2005, https://www.westernite.org/datacollectionfund/2005/psu_ped_summary.pdf
- ↑ Harris, Susan E., "Horse Gaits, Balance and Movement", Turner Publishing Company, 2016
- ↑ https://en.wikipedia.org/wiki/Plotly
- ↑ Holzinger, Andreas and Malle, Bernd and Giuliani, Nicola, "On Graph Extraction from Image Data", Brain Informatics and Health 2014, 552-563, Springer International Publishing
- ↑ https://nefi.mpi-inf.mpg.de/guide.php#limitations, last accessed 2018-12-14