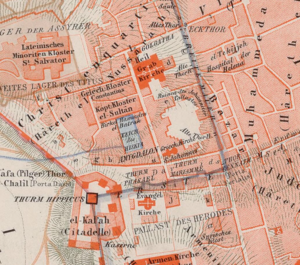
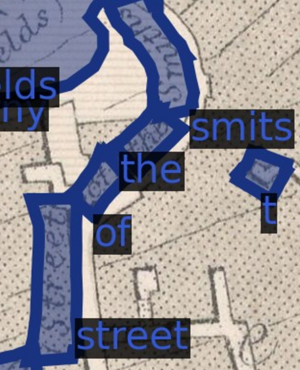
Extracting Toponyms from Maps of Jerusalem: Difference between revisions

From FDHwiki
Jump to navigation Jump to search
Tag: Manual revert
Line 104: Line 104:


==== Word Amalgamation ====
==== Word Amalgamation ====
Let $A_{j} = \{\sigma_{j,1}^{*}, \sigma_{j,2}^{*}, ...,\sigma_{j,r_j}^{*}\}$ refer to the $r_j$ extracted and Text-Rectified labels corresponding to subsets of $G_j$. The goal of the Text Amalgamation stage is to retain a single label from $A_{j}$: the label $\alpha_{j}^{*} = G_{j}$.
This process is performed iteratively. The first step in the amalgamation sequence consists of computing pairwise geometric and textual intersection over minimum (IoM) values between all $\sum_{j=1}^{M}r_j$ labels in the set $R = \{\sigma_{1,1}^*, \sigma_{1,2}^*, ..., \sigma_{1, r_1-1}^*, \sigma_{1, r_1}^*, \sigma_{2, 1}^*, ..., \sigma_{M, r_M-1}^*, \sigma_{M, r_M}^*\}$. For example, suppose we are comparing $\sigma_{a,b}^*$ and $\sigma_{c,d}^*$. In this case, geometric IoM equals $P_{a,b} \cap P_{c,d}$ divided by the area of the smaller polygon. Textual IoM, meanwhile, equals the number of non-unique shared characters in $T_{a,b}$ and $T_{c,d}$ divided by the length of the longer string. Those pairs with geometric IoM value $\gamma_{geom} > 0.75$ and textual IoM value $\gamma_{text} > 0.5$ are considered to exhibit a subset-parent relationship. They are therefore amalgamated, meaning (1) a new label $\sigma_{a,b,c,d}^*$ is added to $R$ with $P_{a,b,c,d} = P_{a,b} \cup P_{c,d}$ and $T_{a,b,c,d} = $ the longer string from $T_{a,b}$ and $T_{c,d}$, and (2) both $\sigma_{a,b}^*$ and $\sigma_{c,d}^*$ are dropped from $R$. When all possible amalgamations have been made based on the group of pairwise combinations satisfying our $\gamma_{geom}$ and $\gamma_{text}$ conditions, the sequence begins anew with updated $R$. The amalgamation stage terminates when $R$ ceases to yield possible amalgamations.
Once both rectification and amalgamation have occurred, the set of labels $L_1, L_2, ..., L_N$ has been condensed to $\alpha_{1}^*, \alpha_{2}^*, ..., \alpha_{M}^*$.
==== Word Combination ====
==== Word Combination ====


Revision as of 22:13, 5 December 2023

Project Timeline

Timeframe Task Completion
Week 4
  • Finalize and present project proposals.
    • Toponym extraction project selected.
 ✓
Week 5
  • Survey SOTA toponym extraction tools.
 ✓
Week 6
  • Port MapKurator's Spotter tool and model weights into Windows-based Python.
  • Select two (later four) maps to use when implementing, evaluating, and fine-tuning MapKurator's model.
 ✓
Week 7
  • Create ground truth labels for first map with VIA's online interface.
 ✓
Week 8
  • Create ground truth labels for second map.
  • Implement 1:1-matched precision and recall via IoU (geometry) and normalized Levenshtein (text).
  • Calculate baseline accuracy statistics.
 ✓
Week 9
  • Implement multi-layer pyramid application of MapKurator's Spotter.
 ✓
Week 10
  • Create ground truth labels for third map.
  • Implement toponym rectification and amalgamation on pyramid-derived toponyms.
 ✓
Week 11
  • Calculate pyramid accuracy statistics.
  • Fine-tune toponym rectification and amalgamation.
  • Deliver Midterm presentation.
 ✓
Week 12
  • Launch Wiki.
  • Group words into toponyms via polygon size and location.
  • Apply NLP tools to correct toponyms based on MapKurator strategy.
Week 13
  • Create ground truth labels for fourth map.
  • Calculate final accuracy statistics.
  • Hierarchize final toponyms and develop Voronoi map.
Week 14
  • Prototype toponym-disagreement visualizer.
  • Finalize Wiki and deliver presentation.

Introduction & Motivation

A sample of the linguistic, geometrical, and typographical diversity in 19th-century maps of Jerusalem.

Methodology

MapKurator

Pyramid

Text Recitification

Let $G_{j,k}$ represent subset $k$ of ground truth label $G_j$. Note that because we do not define $G_{j,k}$ to be a proper subset, it is possible $G_{j,k}$ = $G_j$. Now let the set $S_{j,k} = \{L_1, L_2, ..., L_{p_{j,k}}\}$ refer to the $p_{j,k}$ extracted labels that correspond to $G_{j,k}$ in its entirety. The goal of the Text Rectification stage is to retain the single most accurate extracted label $L_i$ in a given $S_{j,k}$ and exclude the rest - to filter $S_{j,k}$ such that there remains just one `representative' for $G_{j,k}$, in other words.

To organize our extracted labels into the sets $S_{j,k}$, we vectorize each extracted bounding box $P_i$ according to their bottom left and top right cartesian coordinates and implement DBSCAN on the four-dimensional vectors. \textcolor{red}{Tack on DBSCAN hyperparameters. Also, is this still true? ->} Outliers are slotted into their own individual $S_{j,k}$.

To filter our $S_{j,k}$ collections down to their most appropriate representatives, we first attempt to retain the label inside $S_{j,k}$ with the highest $C_i$. \textcolor{red}{Go into RANSACK.}

Let $\sigma_{j,k}^{*}$ be the single label from set $S_{j,k}$ after Text Rectification has occurred.

Word Amalgamation

Let $A_{j} = \{\sigma_{j,1}^{*}, \sigma_{j,2}^{*}, ...,\sigma_{j,r_j}^{*}\}$ refer to the $r_j$ extracted and Text-Rectified labels corresponding to subsets of $G_j$. The goal of the Text Amalgamation stage is to retain a single label from $A_{j}$: the label $\alpha_{j}^{*} = G_{j}$.

This process is performed iteratively. The first step in the amalgamation sequence consists of computing pairwise geometric and textual intersection over minimum (IoM) values between all $\sum_{j=1}^{M}r_j$ labels in the set $R = \{\sigma_{1,1}^*, \sigma_{1,2}^*, ..., \sigma_{1, r_1-1}^*, \sigma_{1, r_1}^*, \sigma_{2, 1}^*, ..., \sigma_{M, r_M-1}^*, \sigma_{M, r_M}^*\}$. For example, suppose we are comparing $\sigma_{a,b}^*$ and $\sigma_{c,d}^*$. In this case, geometric IoM equals $P_{a,b} \cap P_{c,d}$ divided by the area of the smaller polygon. Textual IoM, meanwhile, equals the number of non-unique shared characters in $T_{a,b}$ and $T_{c,d}$ divided by the length of the longer string. Those pairs with geometric IoM value $\gamma_{geom} > 0.75$ and textual IoM value $\gamma_{text} > 0.5$ are considered to exhibit a subset-parent relationship. They are therefore amalgamated, meaning (1) a new label $\sigma_{a,b,c,d}^*$ is added to $R$ with $P_{a,b,c,d} = P_{a,b} \cup P_{c,d}$ and $T_{a,b,c,d} = $ the longer string from $T_{a,b}$ and $T_{c,d}$, and (2) both $\sigma_{a,b}^*$ and $\sigma_{c,d}^*$ are dropped from $R$. When all possible amalgamations have been made based on the group of pairwise combinations satisfying our $\gamma_{geom}$ and $\gamma_{text}$ conditions, the sequence begins anew with updated $R$. The amalgamation stage terminates when $R$ ceases to yield possible amalgamations.

Once both rectification and amalgamation have occurred, the set of labels $L_1, L_2, ..., L_N$ has been condensed to $\alpha_{1}^*, \alpha_{2}^*, ..., \alpha_{M}^*$.

Word Combination

Single Line
Multiple Lines
Curved Line

Evaluation

Results

Limitations

Future work

Github Repository

Jerusalem Maps EPFL DH405

References

Literature

  • Kim, Jina, et al. "The mapKurator System: A Complete Pipeline for Extracting and Linking Text from Historical Maps." arXiv preprint arXiv:2306.17059 (2023).
  • Li, Zekun, et al. "An automatic approach for generating rich, linked geo-metadata from historical map images." Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. 2020

Webpages

Retrieved from "http://fdh.epfl.ch/index.php?title=Extracting_Toponyms_from_Maps_of_Jerusalem&oldid=10280"