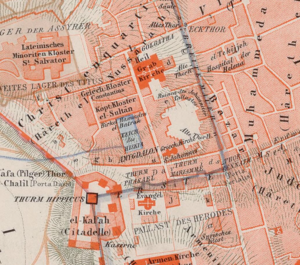
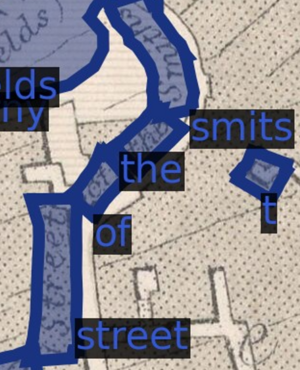
Extracting Toponyms from Maps of Jerusalem

Project Timeline

Timeframe	Task	Completion
Week 4	Finalize and present project proposals. Toponym extraction project selected.	✓
Week 5	Survey SOTA toponym extraction tools.	✓
Week 6	Port MapKurator's Spotter tool and model weights into Windows-based Python. Select two (later four) maps to use when implementing, evaluating, and fine-tuning MapKurator's model.	✓
Week 7	Create ground truth labels for first map with VIA's online interface.	✓
Week 8	Create ground truth labels for second map. Implement 1:1-matched precision and recall via IoU (geometry) and normalized Levenshtein (text). Calculate baseline accuracy statistics.	✓
Week 9	Implement multi-layer pyramid application of MapKurator's Spotter.	✓
Week 10	Create ground truth labels for third map. Implement toponym rectification and amalgamation on pyramid-derived toponyms.	✓
Week 11	Calculate pyramid accuracy statistics. Fine-tune toponym rectification and amalgamation. Deliver Midterm presentation.	✓
Week 12	Launch Wiki. Group words into toponyms via polygon size and location. Apply NLP tools to correct toponyms based on MapKurator strategy.
Week 13	Create ground truth labels for fourth map. Calculate final accuracy statistics. Hierarchize final toponyms and develop Voronoi map.
Week 14	Prototype toponym-disagreement visualizer. Finalize Wiki and deliver presentation.

Introduction & Motivation

A sample of the linguistic, geometrical, and typographical diversity of toponyms in 19th-century maps of Jerusalem.

Methodology

Pyramid

Text Recitification

<math xmlns="http://www.w3.org/1998/Math/MathML" display="block">

 <mi>H</mi>
 <mo stretchy="false">(</mo>
 <mi>P</mi>
 <mo stretchy="false">)</mo>
 <mo>=</mo>
 <mo>−</mo>
 <munder>
   <mo>∑</mo>
   <mrow class="MJX-TeXAtom-ORD">
     <mi>ω</mi>
     <mo>∈</mo>
     <mi mathvariant="normal">Ω</mi>
   </mrow>
 </munder>
 <mi>P</mi>
 <mo stretchy="false">(</mo>
 <mi>ω</mi>
 <mo stretchy="false">)</mo>
 <msub>
   <mi>log</mi>
   <mn>2</mn>
 </msub>
 <mo>⁡</mo>
 <mo stretchy="false">(</mo>
 <mi>P</mi>
 <mo stretchy="false">(</mo>
 <mi>ω</mi>
 <mo stretchy="false">)</mo>
 <mo stretchy="false">)</mo>
 <mo>=</mo>
 <munder>
   <mo>∑</mo>
   <mrow class="MJX-TeXAtom-ORD">
     <mi>ω</mi>
     <mo>∈</mo>
     <mi mathvariant="normal">Ω</mi>
   </mrow>
 </munder>
 <mi>P</mi>
 <mo stretchy="false">(</mo>
 <mi>ω</mi>
 <mo stretchy="false">)</mo>
 <msub>
   <mi>log</mi>
   <mn>2</mn>
 </msub>
 <mo>⁡</mo>
 <mo stretchy="false">(</mo>
 <mn>1</mn>
 <mrow class="MJX-TeXAtom-ORD">
   <mo>/</mo>
 </mrow>
 <mi>P</mi>
 <mo stretchy="false">(</mo>
 <mi>ω</mi>
 <mo stretchy="false">)</mo>
 <mo stretchy="false">)</mo>
 <mo>=</mo>
 <mrow class="MJX-TeXAtom-ORD">
   <mi mathvariant="double-struck">E</mi>
 </mrow>
 <mo stretchy="false">(</mo>
 <mn>1</mn>
 <mrow class="MJX-TeXAtom-ORD">
   <mo>/</mo>
 </mrow>
 <mi>P</mi>
 <mo stretchy="false">)</mo>
 <mo>.</mo>

</math>

Let $G_{j,k}$ represent subset $k$ of ground truth label $G_j$. Note that because we do not define $G_{j,k}$ to be a proper subset, it is possible $G_{j,k}$ = $G_j$. Now let the set $S_{j,k} = \{L_1, L_2, ..., L_{p_{j,k}}\}$ refer to the $p_{j,k}$ extracted labels that correspond to $G_{j,k}$ in its entirety. The goal of the Text Rectification stage is to retain the single most accurate extracted label $L_i$ in a given $S_{j,k}$ and exclude the rest - to filter $S_{j,k}$ such that there remains just one `representative' for $G_{j,k}$, in other words.

To organize our extracted labels into the sets $S_{j,k}$, we vectorize each extracted bounding box $P_i$ according to their bottom left and top right cartesian coordinates and implement DBSCAN on the four-dimensional vectors. \textcolor{red}{Tack on DBSCAN hyperparameters. Also, is this still true? ->} Outliers are slotted into their own individual $S_{j,k}$.

To filter our $S_{j,k}$ collections down to their most appropriate representatives, we first attempt to retain the label inside $S_{j,k}$ with the highest $C_i$. \textcolor{red}{Go into RANSACK.}

Let $\sigma_{j,k}^{*}$ be the single label from set $S_{j,k}$ after Text Rectification has occurred.

<math>G_{j,k}</math>

Text Amalgamation

Let $A_{j} = \{\sigma_{j,1}^{*}, \sigma_{j,2}^{*}, ...,\sigma_{j,r_j}^{*}\}$ refer to the $r_j$ extracted and Text-Rectified labels corresponding to subsets of $G_j$. The goal of the Text Amalgamation stage is to retain a single label from $A_{j}$: the label $\alpha_{j}^{*} = G_{j}$.

This process is performed iteratively. The first step in the amalgamation sequence consists of computing pairwise geometric and textual intersection over minimum (IoM) values between all $\sum_{j=1}^{M}r_j$ labels in the set $R = \{\sigma_{1,1}^*, \sigma_{1,2}^*, ..., \sigma_{1, r_1-1}^*, \sigma_{1, r_1}^*, \sigma_{2, 1}^*, ..., \sigma_{M, r_M-1}^*, \sigma_{M, r_M}^*\}$. For example, suppose we are comparing $\sigma_{a,b}^*$ and $\sigma_{c,d}^*$. In this case, geometric IoM equals $P_{a,b} \cap P_{c,d}$ divided by the area of the smaller polygon. Textual IoM, meanwhile, equals the number of non-unique shared characters in $T_{a,b}$ and $T_{c,d}$ divided by the length of the longer string. Those pairs with geometric IoM value $\gamma_{geom} > 0.75$ and textual IoM value $\gamma_{text} > 0.5$ are considered to exhibit a subset-parent relationship. They are therefore amalgamated, meaning (1) a new label $\sigma_{a,b,c,d}^*$ is added to $R$ with $P_{a,b,c,d} = P_{a,b} \cup P_{c,d}$ and $T_{a,b,c,d} = $ the longer string from $T_{a,b}$ and $T_{c,d}$, and (2) both $\sigma_{a,b}^*$ and $\sigma_{c,d}^*$ are dropped from $R$. When all possible amalgamations have been made based on the group of pairwise combinations satisfying our $\gamma_{geom}$ and $\gamma_{text}$ conditions, the sequence begins anew with updated $R$. The amalgamation stage terminates when $R$ ceases to yield possible amalgamations.

Once both rectification and amalgamation have occurred, the set of labels $L_1, L_2, ..., L_N$ has been condensed to $\alpha_{1}^*, \alpha_{2}^*, ..., \alpha_{M}^*$.

Word Combination

Single Line

Multiple Lines

Curved Line

Github Repository

Jerusalem Maps EPFL DH405

References

Literature

• Kim, Jina, et al. "The mapKurator System: A Complete Pipeline for Extracting and Linking Text from Historical Maps." arXiv preprint arXiv:2306.17059 (2023).
• Li, Zekun, et al. "An automatic approach for generating rich, linked geo-metadata from historical map images." Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. 2020

Webpages

• MapKurator GitRepo
• MapKurator Introduction