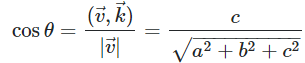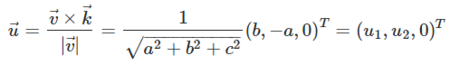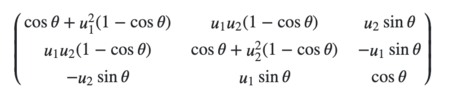Venice2020 Building Heights Detection
Introduction
The main goal of our project is to obtain the height information of buildings in Venice. In order to achieve this goal, we construct a point cloud model of Venice with drone video from youtube and google earth with the help of a photogrammetry tool developed at DHLAB.
Motivation
Building height is one of the most important information to consider for urban planning, economic analysis, digital twin implementation, and so on. For Time Machine implementation, it is important to compare different historical data and current data based on different times. Drones and Google Maps provide 3D views of buildings and surroundings in detail which are useful resources to keep track of changes in a target place. In this project, we aim to detect the building heights of Venice. Many geographical areas, which are either not famous or not accessible easily are accessible by Google Earth 3D views. We aim to make a 3D model of Venice with every detail of the city and calculate point clouds to detect the heights of the city. This information can be used to understand current details of the city and also will be useful in the future as historical data to compare with.
Methodology
Images Aquisition
Point cloud denotes a 3D content representation which is commonly preferred due to its high efficiency and relatively low complexity in the acquisition, storage, and rendering of 3D models. In order to generate Venice dense point cloud models, sequential images from different angles in different locations need to be collected first based on the following two sources.
Youtube Video Method
Our initial plan was to download drone videos of Venice on the Youtube platform, used FFmpeg to extract images from the video one frame per second, and generate dense point cloud models based on the images that we acquired. However, the videos we could get from drone videos are very limited: only a few of the videos are of high quality. Among those qualified videos, most videos only focused on monumental architecture such as St Mark's Square, St. Mark's Basilica, and Doge's Palace, where other buildings have a different extent of deficiencies from various angles in the point clouds. Therefore, a large proportion of Venice could not be 3D reconstructed if we only adopt Youtube Video Method.
Google Earth Method
In order to access the comprehensive area of Venice, we decided to use Google Earth as a complementary tool: we could attain images of every building we want at each angle. With Google Earth, we are able to have much more access to aerial images of Venice, not only will these images serve as images set to generate dense point cloud models in order to calculate building heights, but we can also use the overlapping part in different point cloud models to evaluate point cloud models in a cross-comparison way.
In a nutshell, we apply a photogrammetric reconstruction tool to generate point cloud models. Photogrammetry is the art and science of extracting 3D information from photographs. As for the Youtube-based method, we will only target famous buildings which appear in different drone videos and select suitable images to form the specific building's image set. With regard to the Google Earth method, we will obtain images of the whole of Venice manually in a scientific trajectory of the photogrammetry route.
Point Cloud Processing
Outlier Removal
Error Reduction
The first phase of error reduction is to remove points that are a result of poor camera geometry. Reconstruction uncertainty is a numerical representation of the uncertainty in the position of a tie point based on the geometric relationship of the cameras from which that point was projected or triangulated, considering geometry and redundancy. Reconstruction uncertainty can also be thought of as the ratio between the largest and smallest semiaxis of the error ellipse created when triangulating 3D point coordinates between two images. Points constructed from image locations that are too close to each other have a low base-to-height ratio and high uncertainty. Removal of these points does not affect the accuracy of optimization but reduces the noise in the point cloud and prevents points with large uncertainty in the z-axis from influencing other points with good geometry or being incorrectly removed in the reprojection error step. A reconstruction uncertainty of 10, which can be selected with the gradual selection filter and set to this value or level, is roughly equivalent to a good base-to-height ratio of 1:2.3 (parallax angle of about 23 degrees [°]), whereas 15 is roughly equivalent to a marginally acceptable base-to-height ratio of 1:5.5 (parallax angle of about 10°). Previous guidance directs the reconstruction uncertainty selection procedure to be repeated two times to reduce the reconstruction uncertainty toward 10 without having to delete more than 50 percent of the tie points each time. If a reconstruction uncertainty of 10 is reached in the first selection attempt and less than 50 percent of the tie points are selected, a single optimization after deleting points is sufficient.
The second error reduction phase removes points based on projection accuracy, which is a measure of the “Mean key point size”; the value is accessed from the chunk information dialog. The key point size (in pixels) is the standard deviation value (in σ) of the Gaussian blur at the scale at which the key point was found; lower standard deviation values are more precisely located in space. Thus, the smaller the mean key point value, the smaller the standard deviation and the more precisely located the key point is in the image. Projection accuracy is essentially a representation of the precision with which the tie point can be known given the size of the key points that intersect to create it. Metashape saves an internal accuracy and scale value for each tie point as part of the correlation process. The highest accuracy points are assigned to level 1 and are weighted based on the relative size of the pixels. A tie point assigned to level 2 has twice as much projection inaccuracy as level 1. Not all projects can tolerate gradual selection and removing points at a level of 2 to 3, particularly if the images have undergone compression or are of lower quality from noise or blur. A gradual selection level of 5 or 6 may be the best that can be obtained. Previous guidance directs the projection accuracy selection procedure is to be repeated without having to delete more than 50 percent of the points each time until level 2 is reached, and at this level, there are few to no points selected. Here we clarify that after level 3 is reached, repeated selections have diminishing returns and the added optimizations may overfit the camera.
The final error reduction phase is removing points based on reprojection error. This is a measure of the error between a 3D point’s original location on the image and the location of the point when it is projected back to each image used to estimate its position. Error-values are normalized based on key point size (in pixels). High reprojection error usually indicates poor localization accuracy of the corresponding point projections at the point matching step. Reprojection error can be reduced by iteratively selecting and deleting points, then optimizing until the unweighted RMS reprojection error (in pixels) is between 0.13 and 0.18 with additional optimization coefficients checked and with the use of the “Fit additional corrections”. The weighted RMS reprojection error is calculated such that not all points selected by targeting a specific reprojection error level will remove the same level of estimated error. When a value of 0.13 to 0.18 unweighted RMS reprojection error (in pixels) is reached, there is 95% confidence that the remaining points meet the estimated error. Most projects should be sufficiently optimized at a reprojection error of 0.3 pixels, and there should be no noticeable differences in products with additional optimization. However, high-quality images may benefit from more rigorous error reduction to the lower levels and produce a better camera calibration. At this step, the tie point accuracy (in pixels) could also be revisited (step 8), while constantly monitoring the camera and marker total errors to assist in the decision to stop the error reduction and optimization process.
Plane Generation
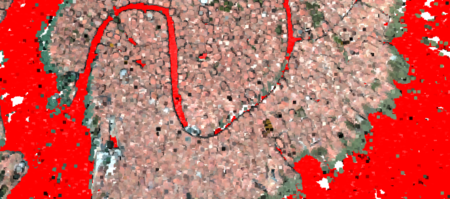
To calculate the height of the building, we have to find the ground of the PointCloud model, which could be retrieved by a tool provided by Open3D. Open3D supports segmentation of geometric primitives from point clouds using 'Random Sample Consensus', which is an iterative method to estimate parameters of a mathematical model from a set of observed data that contains outliers when outliers are to be accorded no influence on the values of the estimates. To find the ground plane with the largest support in the point cloud, we use segment_plane by specifying 'distance_threshold'. The support of a hypothesized plane is the set of all 3D points whose distance from that plane is at most some threshold (e.g. 10 cm). After each run of the RANSAC algorithm, the plane that had the largest support is chosen. All the points supporting that plane may be used to refine the plane equation, which is more robust than just using the neighboring points by performing PCA or linear regression on the support set.
Plane Redress
After selecting the most convenient plane and its supporting points, we define the plane equation in the 3D space. We want to build a PointCloud model where the Z coordinate of a point equals the height of this point in real world, so the next step is to redress the plane by projecting it on an X-O-Y space. For the projection calculation, we used the projection matrix mentioned in fig 3.
Here, the plane equation is,
ax + by + cz + d= 0
The redressing was performed in two steps, first translation and then rotation.
For translation, let, the plan intersects Z-axis at (0, 0, -d/c). So the translation is
which passes through the origin and vector v = (a, b, c)T
For the rotation, the angle between v and k = (0, 0, 1)T is,
The axis of rotation has to be orthogonal to v and k. so its versor is:
Here,
u1 = b / √(a2 + b2 + c2)
u2 = -a / √(a2 + b2 + c2)
sinθ = √( (a2 + b2) / (a2 + b2 + c2) )
cosθ = c / √(a2 + b2 + c2)
Model Scaling
The highest building in Venice is 98.6 meters. To make the model height the same as the height in real life, we have applied Plane Scaling. In order to do this, Z coordinates of the points were made equal to the real height of the building. Scale function and rotate function from Open3D were used for the calculation. To align the model in the right position, we have applied the translation rotation method in an iteration loop of 1000. The scale factor is
real height/height in the model
Point-to-Plane Based Height Calculation
Once the plane equation is obtained in the previous step, we could start calculating the height of buildings.
In the first step, we calculate the relative height of the buildings based on the formula of point-to-plane distance. The coordinate information of each point was accessed by the 'points' property of the ‘PointCloud’ object with the help of 'Open3D'. Since we already have the plane equation, using this formula, we obtain the distance between each point and the plane.
In the second step, we use mapping to calculate the real height of the buildings. For instance, we know the real height of St. Mark Basilica, and we already calculated the relative height of St. Mark Basilica, therefore, we could obtain the scale factor in this PointCloud model. Then, for all the other buildings in the model, the real height of the building = the relative height of the building * scale factor.
City Elevation Model Construction
To visualize the height of the building, we are going to build height map.
Nevertheless, we do not have the 2D coordinate information of the points since the PointCloud is a three dimentional object and the plane equation doesn’t match the plane in the coordinate system, we could not just plot the height information on a 2D map. An alternative visualization method is to express the height information of each point through the ‘Colors’ attribute of the ‘PointCloud’ object.
For each point in the ‘PointCloud’, it has a ‘Colors' attribute, by calling it, an array of shape (n, 3), value range [0, 1], containing RGB colors information of the point will be returned. Therefore, by normalising the ‘distance array’ value to the range of [0,1], and expanding the distance array to three dimensions by replication, we get a ‘height array' of shape (n, 3) in the form of 'colors array’.
Cadaster Alighment
Quality Assessment
Limitations
- In the very beginning, our initial plan was to detect building heights bases on PointCloud models generated by Youtube drone videos. Nevertheless, only a few of the videos are of high quality. Among those qualified videos, most videos only focused on monumental architecture such as St Mark's Square, St. Mark's Basilica, and Doge's Palace, where other buildings have a different extent of deficiencies from various angles in the point clouds. Therefore, a large proportion of Venice could not be 3D reconstructed if we only adopt Youtube Video Method.
- Using google Earth images is a solution to the problems mentioned above. But it is not a perfect method either. We seem to be in a dilemma when we tried to collect images from Google Earth: When we took screenshots from a long distance from the ground, the resolution of images are very low, the details of the buildings are not well rendered, thus causing the low quality of the PointCloud. When we took screenshots from a short distance from the ground, we get a much better result, the details are much more clear, but to achieve this, the number of images we need to build the PointCloud models increase exponentially, and the calculation is almost impossible for a Personal Computer to afford. One possible solution is dividing Venice into smaller parts, build a PointCloud for every part and merge the PointClouds. This solution might require alignment, which isn't precise, and well-know for being hard to implement.
- Plane Generation
Plane Generation isn't perfect.
- When we implement 'Plane Redress', the ideal scenario is that after transformation, the plane equation should be 0*x + 0*y + c*z = d. However, when we implement the transformation, the coefficients before x and y are not exactly 0, even though they get closer to 0 after each iteration.
Milestones
Milestone 1
- Get familiar with OpenMVG, Open3D, OpenGM, Point Cloud Library, Agisoft Metashape, Blender, CloudCompare and QGIS
- Collect high resolution venice drone videos on youtube and record Google Earth birdview videos as supplementary materials
Milestone 2
- Align photos of the same location in Venice, derive sparse point clouds made up of only high-quality tie points and repeated optimize the camara model by reconstruction uncertainty filtering, projection accuracy filtering and reprojection error filtering.
- Build dense point clouds using the estimated camera positions generated during sparse point cloud based matching and the depth map for each camera
- Evaluate point clouds objective quality and select high quality models by point-based approaches which can assess both geometry and color distortions
Milestone 3
- Align and compose dense point clouds of different spots to generate an integrated Venice dense cloud model (implement registration with partially overlapping terrestrial point clouds)
- Build Venice 3D model (mesh) and tilted model according to dense point cloud data
- Generate plane of the surface ground
Milestone 4
- Build the digital elevation model of Venice and align the model with open street map and cadaster in the 16th century to obtain building heights
- Assess the accuracy of the building heights detection
Planning
| Week | Tasks | Completion |
|---|---|---|
| week 5 |
|
✓ |
| week 6-7 |
|
✓ |
| week 8-9 |
|
✓ |
| week 10 |
|
✓ |
| week 11 |
| |
| week 12 |
| |
| week 13 |
| |
| week 14 |
|