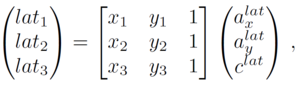Shortest-Path Route Extraction From City Map

The Historical Document

Original map which forms the basis of the project. Note the distinction between already built sections (darker, south-west) and unfinished or planned sections (lighter, north-east).

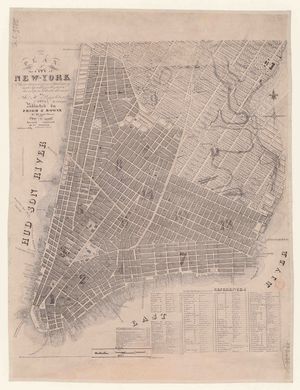
We are working on a historical map of Manhattan, depicting mostly Lower Manhattan as well as some part to the north-east side. The following is a compilation of some contextual information retrieved directly from within the map:

• Self-designated as "Plan of the City of New-York"
• Published in 1829
• In the English language
• Source material of the map states: "The greater part from actual survey made expressly for the purpose (the rest from authentic documents)"
• By Thomas H. Pappleton, City Surveyor
• Published by Prior & Bowne
• Revised and corrected by William Hooker

The map features a clear visual distinction between two sections. The first one, delimited to the north-east by North Street, Bowery, Eighth Street, Greenwich Lane, and Great Kill Road, is characterized by buildings drawn shaded-in. This is in contrast to the other section, where buildings are drawn more lightly. Places that are superimposed over roads are drawn in a dashed style. The former section depicts parts of the city that are already built, while the latter represents parts that are unfinished or only at a planning stage. While this interpretation is natural, it is not evident beyond doubt from the map itself (which lacks a legend) what the meaning of the different shadings of the buildings is. However, another map from around the same time (1836), allowed us to draw this conclusion. This other map contains a broadly similar division, as well as a legend revealing the darker areas as "section[s] of city built" and the lighter ones as either "opened or being regulated" or "established by ordinance".

For the project, only the darker section on the map, corresponding to already built parts of the city, is used - the rest is ignored.

Extraction methods

Graph extraction

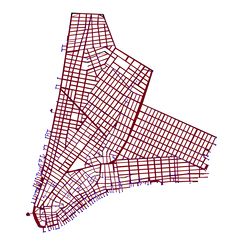
For the proposed application, the relevant information that needs to be extracted from the map is a usable representation of the road network. For this, the Python tool NEFI (Network Extraction From Images), developed at Max Planck Institut für Informatik, is used. The tool performs automated detection of networks in images based on the Guo-Hall thinning algorithm and outputs the extracted network as an undirected planar graph, stored in a text file. Intersections are the nodes of the graph in this representation, while roads are edges. Besides the fundamental graph extraction step, the tool also provides functionality for some basic image preprocessing before graph extraction, as well as some options for post-processing the extracted graph.

However, simply running NEFI on the map image, as it is, is not enough to get satisfactory graph extraction results. In fact, for the application at hand, nothing less than an optimal graph is acceptable since a graph where edges and nodes do not accurately coincide with roads and intersections will be either unsuitable for direction-finding or at least visually displeasing when overlaying computed routes onto the map image. A desirable workflow for the whole graph extraction process might look like this:

• Crop the image, remove from the outset portions of the image that are irrelevant (in this case: margins, sea, sections corresponding to parts of the city not yet built), basic image preprocessing (e.g. enhance contrast, blur). While the latter could be achieved using NEFI's inbuilt preprocessing capabilities, these are fairly limited, so using an external program is likely advisable.
• Automated graph extraction using NEFI.
• Visually assessing and, as required, manually correcting inaccuracies in the graph extracted from the map. For this task, ideally, we would need a GUI tool that provides the possibility to overlay the graph onto the original map and, directly in this view, permit manual editing of nodes and their connections in accordance with the underlying image.

Map that was manually segmented into roads (black) and inaccessible areas (white), with the graph extracted overlaid on top. Blue: nodes. Red: edges.

Unfortunately, no such convenient way of correcting errors in the extracted graphs by means of a graphical editor was found. This leaves us with no option for correcting graph errors but editing directly the text file in some way, which is highly impractical. As a result, the preprocessing and cleaning of the image before graph extraction becomes all the more important. To get decent results, we had to resort to rather heavy preprocessing, manually segmenting the image into roads and inaccessible areas (i.e., coloring them black and white, respectively) using GIMP (Gnu Image Manipulation Program). Graph extraction using NEFI is then run on the manually segmented image. The pipeline that was specified in NEFI consists of the following ordered steps:

• "Watershed DE Otsus" from category Segmentation, short for "Watershed with Dilation, Erosion and Otsu’s Threshold". Default settings are used.
• "Guo Hall Thinning" from category Thinning. This algorithm does not have any settings.
• "Guo Hall Graph Detection" from category Graph Detection. This algorithm does not have any settings.
• "Keep only LCC" from category Graph Filtering. This removes all but the longest connected components from the graph obtained. This algorithm does not have any settings.

We realize this approach is far from ideal, and not very efficient, since the manual segmentation in the preprocessing step actually amounts to (implicitly) doing a big part of the graph extraction by hand, but the indirect route via NEFI still has to be taken for the actual graph extraction. We nonetheless decided to stick to that approach, since it works in principle, and spending more time searching for a user-friendly tool for manual extraction and editing of graphs based on images was deemed not worthwhile. However, for future similar projects, it might be advisable to invest some time in researching, or even creating, such a tool. Having such a tool at one's disposal, one could perform manual graph extraction conveniently: forgoing the indirect route via NEFI entirely. Alternatively, you could cut down on the necessary preprocessing before the automated graph extraction via NEFI, since there would now be a feasible way of correcting errors afterwards.

Additionally, the manual segmentation during the preprocessing inevitably introduces some human-input-related ambiguity. However, this is not inherently different from the ambiguity that would arise in direct manual graph extraction or the ambiguity involved with assessing the accuracy of an extracted graph. Some degree of ambiguity of this type therefore seems unavoidable.

Relating to real-world coordinates and distances

Map with the reference and checking points highlighted that were manually matched to real-world coordinates. Green: The three reference points based on which the conversion parameters were computed. Red: Additional 12 points used for quantifying the inaccuracy of that conversion.

The output we get from NEFI, as detailed in the previous section, is a planar representation of the road network, where the coordinates of nodes correspond to pixel coordinates in the image from which the graph was extracted. A priori, this is not meaningful. To make those coordinates meaningful, we need to link them to real-world coordinates and distances.

We briefly explored the idea of using georeferencing by means of the software QGIS to help us with this. However, we could not find any information on the reference ellipsoid and projection system used in the historical map, which is information required information for georeferencing. Additionally we encountered what might be a bug in QGIS (but might also be merely incorrect usage) where raster maps above a certain size (pixel number, not file size) are not displayed correctly in the program. We therefore abandoned this idea.

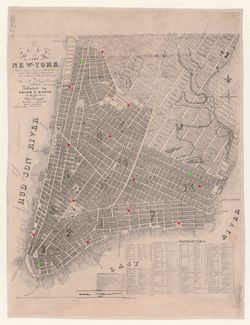
Instead, we decided to approximately solve these problems by assuming a linear transformation between graph and real-world quantities (i.e. disregarding all curvature effects) and explicitly working out by ourselves the conversion factors involved. Later, we will give an estimate of the error caused by this linearization. The first step in this process is to find three reference intersections, that are clearly identifiable both on the historical map and on a modern map. For these three reference intersections, the coordinates of the corresponding nodes on the graph, and their real-world latitude and longitude (read manually from Google Maps) are registered.

For converting the coordinates of graph nodes to real-world latitude and longitude, we assumed the linear relations

with coefficients a_x^lat, a_y^lat, c^lat, a_x^long, a_y^long, c^long to be determined. To that end, we solved the system of linear equations (shown only for latitudes, but it works anaologously for longitudes)

where (x_i, y_i), i=1,2,3, are the graph coordinates of the three reference intersections and lat_i are their latitudes in degrees.

For calculating the real-world distance between two points in the graph coordinate system, we employ the first-order approximation

where d_real is the real-world distance along geodesics, d_graph is the 2-norm of the difference between two points in the graph coordinate system, and alpha is a uniform scale factor between them. To find the scale factor, we are then simply taking the ratio d_real/d_graph. In principle, it is sufficient to do this for only one reference distance. However, we did it for all three sides of the triangle formed by the three reference intersections, followed by taking the mean, to make the result less susceptible to possible inaccuracies in identifying the matching points between the historic and modern map. To compute the real-world distances d_real, we used Wolfram Mathematica's GeoDistance function, which takes curvature effects into account.

While the conversion from graph coordinates to latitude/longitude and the conversion from graph distances to real-world distances are based on the same three reference points, the two conversions are otherwise independent and do not make use of each other. The conversion to latitude and longitude is in fact only used for displaying positions when hovering over the map with the cursor, and for displaying coordinates of destinations in the sidebar on the webpage.

Quantitative analysis of extraction performance

Linearization errors

To quantify the errors incurred by linearizing the dependence of latitudes/longitudes and real-world distances on the graph coordinates, we selected another twelve matching points on the historic and a modern map (Google Maps), and noted their graph node coordinates and corresponding real-world latitude/longitude. This is on top of the three reference points already selected for computing the conversion parameters. We tried to select those twelve points used for checking in such a way that they are more or less evenly distributed across the map. However, we did not have total liberty to do so, since not all features visible on the historical map are still present in modern-day New York, forcing us to slightly restrict our choice.

The follwing table shows the real latitudes and longitudes of the twelve points, and the errors of the computed latitudes and longitudes with respect to real-world ones. We find that the maximum error (by absolute value) is 0.000274527° for the latitudes and 0.000342848° for the longitudes.

number of checking point	latreal [degrees]	longreal [degrees]	latcomputed - latreal [degrees]	longcomputed - longreal [degrees]
1	40.714186	-74.006306	-0.000189	-0.000275
2	40.711329	-73.983644	-0.000074	-0.000343
3	40.718167	-73.993845	-0.000103	-0.000251
4	40.717533	-73.980001	-0.000009	-0.000032
5	40.708233	-74.014393	-0.000279	-0.000245
6	40.707226	-74.002751	0.000101	-0.000256
7	40.723291	-74.008029	-0.000165	-0.000251
8	40.730166	-73.996082	0.000082	-0.000016
9	40.732668	-74.008626	-0.000076	-0.000230
10	40.738769	-74.002449	0.000041	0.000171
11	40.725006	-73.999357	-0.000082	-0.000213
12	40.713022	-73.994455	-0.000137	-0.000256

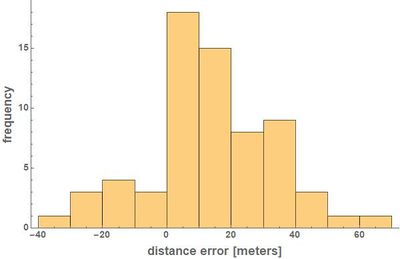
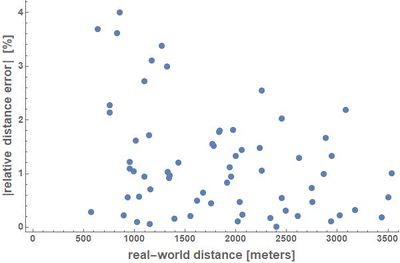
Next, we turned our attention to the errors in the distance calculations. From the twelve control points chosen, 66 unordered pairs of points can be formed. For these 66 pairs, we calculated the real-world distances d_real (using Wolfram Mathematica's GeoDistance function) and the distances d_computed that our approximative method gives us, and then calculated the errors d_computed - d_real. The maximum error (by absolute value) found among the 66 pairs of points was 67.402 meters. To put this into perspective, if we assume that the typical extent of an intersections is between 10 and 20 meters along both directions, then we can note that the linearization error, while it cannot be explained by the inaccuracy or uncertainty alone that can be ascribed to defining an intersection's position, is at least on the same order of magnitude. The following figures visualize the distribution of the distance errors found as a function of the real distances between points.

Histogram showing the frequency distribution of different values of the distance error, for all 66 points of pairs analyzed. Note how there is bias towards positive distance errors, i.e, our compuation method tends to overestimate the real-world distance more often than underestimate it.

Absolute values of relative distance errors, expressed as percentages, plotted over the real-world distances for all 66 points of pairs. The largest relative distance errors are in fact observed at the lower end of the distance range. This might be due to the fact that the scale factor relating graph and real-world distances was computed for pairs that are rather far apart.

Project Plan and Milestones

Note that, by design, this section is a snapshot of the project planning at an intermediary stage (as of November 14), and therefore might not accurately reflect all steps taken at later stages.

Our final goal is to create a simple Google-Maps-style navigation tool for the past. The user will be able to select two points, and see the shortest path between these two points. This would be useful for someone to estimate how they would navigate through a city - possibly hundreds of years ago. Florian has been tasked with pre-processing the historical map. This involves searching for the best maps and cleaning them. Cleaning is crucial to ensure that an accurate graph is extracted from the map. Jonathan is working on representing the graph visually, creating interactivity, and hosting it on a website.

Already Completed

• Researched software that will help us with graph extraction

• Took the first steps to developing a cleaning process for each map

• Written Python code to display a graph from a text list of nodes and edges

• Completed simple routing between two nodes

• Setup a website and domain (www.dhproject.cf) to showcase our project

Future Goals

• Take a decision on which overall direction to pursue for the remainder of the project: Generality, by including several other maps? Or, adding selection of start and end point based on address input, to more closely mimic the interface and functionality of services like Google Maps? (November 23)

• Letting a user select two nodes on the map, and displaying the shortest path between the two nodes. (November 23)

• Displaying the interactive graph on the website. (November 23)

• Calculating and displaying the actual estimated distance between the two points. (end of November)

• Overlay the graph representation onto the historical map. (end of November)

• Develop a manual process for assessing how accurate graph extraction is, and correcting if necessary. (end of November)

• Some buffer time, to allow for unforeseen work. (December 1 to 9)

• Finish Wiki writing (December 12)

• Refine (and automate) the cleaning process. This may involve researching other maps and choosing the best ones for our needs. (no hard time frame, depending on feasibility and necessity)

• Possibly move the network extraction, which is currently done via GUI, to a script. (no hard time frame, depending on feasibility and necessity)

• (Stretch goal) Allow a user to upload their own map which will be processed and displayed.

Links

• Project website
• Github repository