Completing Facades

Introduction

Venice is a unique city with both cultural and historical significance. Digital copies of cities allows us to preserve and understand them better. Photogrammetry is a technology that can be used to do this which uses images and scans to create models of real world objects and sites. However, due to the nature of the technology there are often holes, missing regions and noise in the data. This project aims to fill in holes in data from photogrammetry of facades in Venice by also using historical data over buildings in Venice. For this 2D images from photogrammetry of Venice is used. The dataset used includes completed and incomplete facades. To achieve this aim a method for generating artificial holes in facades was developed together with a dataset of facades with artificial holes and the binary mask for the created missing regions. A machine learning method for detecting the holes in the facades was developed. Additionally, two methods for alining footprints of Venice buildings was implemented and evaluated in order to align a hand drawn map with the footprint of Venice. Finally, we tried several inpainting methods to fill holes and analyzed their differences. The methods used included Stable Diffusion, LaMa, and PartialConv. Based on our tests, we selected the model most suitable for our tasks—one capable of handling low resolution, filling large holes, and fine-tuned it using our custom validation dataset. Additionally, we trained a model from scratch.

Motivation and description of the deliverables

Dataset with generated holes

This data set was created in order to train a model on detecting holes. This dataset acts as a validation dataset. It is made up of a subset of about ~1000 facades which are nearly complete. Each facade is then used to generate 6 more datapoints, with 1-6 artificial holes.

Model for identifying holes

This model was created in order to fill the missing regions of facades. We use this to prevent noise, filling or reconstructing regions which we are not wanting to reconstruct.

Models to fill in holes

We would like to try several different models which should be suitable for our dataset since our pictures' resolutions are considerably low and some of them have very large holes. We used multiple different methods for hole reconstruction while we split those methods into two categories: data-variant and data-invariant. Data-Invariant methods do not use our existing dataset. They generate solutions independent of our data. While Data-Variant methods do use our existing dataset. They generate solutions based on our data.

Method for filtering and shifting cadastre data

This algorithm is used to re-align cadastre data with modern building footprints. It is used to be able to connect the historical data to the facades of Venice.

Sorted facades by attributes

This dataframe contains attribute assignments for all the facades. These attributes are:

1. Sestiere
2. Percentile in the distribution of Facade Area (m2)
3. Usage Types
4. Ownership Types

Project Timeline & Milestones

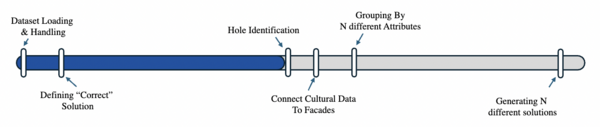
For this project, GitHub served as the project management tool. It was used to organize tasks, track progress, and develop a project timeline. The first week of the project was spent setting up our environments, loading in the data for the project and exploring it. This work continued in the second week and we also started to define our pipeline for reconstructing the facades. The fist step of the pipeline which we identified was to be able to identify where the holes are in the facade. Therefore, we started working on this. To optimize our work we also started working on attaching the cadastre data to the facades and then preparing for the presentation. The project timeline was structured around specific milestones for after the midterm presentation in order to complete the pipeline for filling in the identified holes in the facades. Figure 2.1 illustrates the progress of tasks before the midterm presentation and the milestones after the midterm presentation.

Figure 2.1: Timeline over project from midterm presentation

Three major milestones were defined for the remaining work together with writing and preparing for the final presentation.

The first milestone:

• Completing the detection of holes in facades
• Completing attaching cadastre data to the building footprints
• Literature review of hole filling methods

The second milestone:

• Group facades by attributes
• Start exploring and developing hole filling methods

The final milestone:

• Development and refinement of the model to fill in the detected holes in the facades
• Writing and preparing for the presentation

The table below shows a weekly project overview.

Project timeline

Week	Task	Status
07.10 - 13.10	Set up python environments, explore dataset, structure work on Github	Done
14.10 - 20.10	Document and explore dataset and start defining pipeline	Done
21.10 - 27.10	Autumn vacation	Done
28.10 - 03.11	Work on detecting holes, attaching cadastre data to footprints of Venice	Done
04.11 - 10.11	Work on detecting holes, attaching cadastre data to footprints of Venice.Prepare for the presentation	Done
11.11 - 17.11	Midterm presentation on 14.11. Finish attaching cadastre data to footprints of Venice and hole detection method.	Done
18.11 - 24.11	Finish attaching cadastre data to footprints of Venice and hole detection method.Litterature review of hole filling method	Done
25.11 - 01.12	Sort and group facades by different attributes, work on hole filling method, start writing.	Done
02.12 - 08.12	Sort and group facades by different attributes, work on hole filling method, start writing	Done
09.12 - 15.12	Finish writing wiki, Prepare presentation
16.12 - 22.12	Deliver GitHub + wiki on 18.12 Final presentation on 19.12

Methodology

All of our methodology is best described in the relevant git issues.

In order to fill the holes in the images they first need to be detected. We will do this by generating binary masks of the size of the image, where "1" in the mask indicates a hole pixel which is missing data. Missing data is always black, but black pixels are not always missing data. Thus, we need to categorize black pixels into different types of "missing" and decide which of these types should be filled.

These missing region types are:

1. Photogrammetry Noise
2. Obstruction by Geometry
3. The sky
4. Intersection of Facades

Photogrammetry noise are those pixels which are obstructed by micro-geometries in the current facade, and appear as pixelated noise. Obstruction by geometry regions are large regions of black pixels where a large geometry, such as another building, has blocked the aerial photogrammetry from capturing the relevant facade. Both of these regions are due to failings in the data collection process, and need to be simulated/filled in.

The sky is any pixel outside of the current facade. It is caused by the fact that binned facade images do not fit completely inside a rectangle image. Thus, *the sky* is essentially just padding around a supposedly complete facade. Facade intersections are black regions caused by another building touching the relevant facade. This is the toughest region to identify. Neither of these regions should be simulated, as in reality there is no data there.

So, our goal will be to first identify the photogrammetry noise, geometry obstruction, and facade intersection regions together. This will get rid of the sky from our masks. Then, we will remove the facade intersection region from our predicted hole region. At the end of our pipeline, we will just be left with the two regions we want to simulate: photogrammetry noise and geometry obstruction.

In order to remove the sky, we will train a machine learning model to identify the three other types of missing regions. In order to train such a model, however, we need a training dataset. This doesn't exist with the original data, so we need to create our own.

Creating training/validation data

In order to create our validation set, we need to artificially create holes in facades which do not have any other holes. So, we first sub-selected ~1000 facades with >95% "percentage filled" metric from the original dataset. It isn't clear how this metric was computed, and indeed the original hole predictions from the dataset are not correct. However, we are just looking for completeness, so this rough metric will do. We will call this subset of about ~1000 facades the "Nearly Complete" subset.

Now, we need to create artificial holes in our dataset, and keep track of where these holes are in the facade images. These holes need to be realistic enough so a model trained on our artificial dataset is able to predict real holes in the real dataset. We derived the following algorithm for creating a realistic artificial hole:

Algorithm CreateArtificialHole
Input:
   bd - Image data
   n_holes - Number of holes
   hole_size - Size per hole (fixed or range)
   epsilon - Probability threshold
Output:
   bd with 'is_hole' marked for hole pixels
BEGIN
   // Initialize 'is_hole' column
   bd['is_hole'] ← False
   FOR i FROM 1 TO n_holes DO
       // Determine hole size
       IF hole_size is range THEN
           size ← Random(min, max)
       ELSE
           size ← hole_size
       END IF
       // Select starting pixel
       start ← RandomPixel(bd WHERE not bd['is_hole'])
       bd[start].is_hole ← True
       hole_pixels ← [start]
       // Define neighbor directions
       directions ← [left, right, up, down]
       // Grow the hole
       WHILE Length(hole_pixels) < size DO
           new_pixels ← []
           FOR pixel IN hole_pixels DO
               FOR direction IN directions DO
                   neighbor ← GetNeighbor(pixel, direction)
                   IF neighbor exists AND not bd[neighbor].is_hole THEN
                       prob ← epsilon + bd[neighbor].gradient
                       IF Random() > prob THEN
                           bd[neighbor].is_hole ← True
                           new_pixels.append(neighbor)
                       END IF
                   END IF
               END FOR
           END FOR
           hole_pixels.extend(new_pixels)
           // Early termination chance
           IF Random() < 0.0001 THEN
               BREAK
           END IF
       END WHILE
   END FOR
   // Post-processing: Remove a small fraction of hole pixels
   sampled ← Sample(bd WHERE bd['is_hole'], fraction=0.01 to 0.05)
   FOR pixel IN sampled DO
       bd[pixel].is_hole ← False
   END FOR
   RETURN bd
END Algorithm

This was ran with an `n_holes` value of 6.

Thus, we have a dataset with features being facades with realistic holes and labels being binary masks indicating where the holes are.

• 

  Sampling Locations for a New Hole

• 

  Growing along Sobel gradients of a Facade

• 

  Adding Noise Back into a Grown Hole

• 

  An example "nearly-complete" facade to use for the validation set.

• 

  A generated hole mask for this image.

• 

  The resulting datapoint for our validation training set.

Method for Detecting Holes

After creating our dataset, we then train a model for semantic segmentation of facade images into holes and non-holes. For our approach, we used a U-Net style architecture. For our encoder, we used a pre-trained MobileNetV2. We trained our own decoder. Our model would then output per-pixel probabilities of being a hole. We then applied a liberal threshold to these probabilities to get a hole mask which excludes the sky.

The UNet Architecture for Identifying Holes.

[[

Different Thresholds for Hole Prediction.

We then process the predicted hole-masks by removing any geometry intersection regions. We use the following algorithm to do this:

Algorithm ProcessFacadeMask
Input:
  FacadeID - Identifier for the facade
Output:
  Final mask for the FacadeID
BEGIN
  // Step 1: Calculate the intersection of footprints
  intersection ← CalculateIntersection(FacadeID)
  // Step 2: Filter facades with the most area in the intersection bounding box
  top_facades ← SelectTopFacades(intersection, n=2)
  // Step 3: Process each intersection
  FOR facade IN top_facades DO
      // Load building data and convert it to image representation
      building_image ← LoadBuildingData(facade)
      // Generate masks with a low threshold using a model
      mask ← GenerateMask(building_image, threshold="low")
      // Flip and resize the mask of the intersected neighbor facade
      neighbor_mask ← FlipMask(mask)
      neighbor_mask ← ResizeMask(neighbor_mask, size=Size(building_image))
      // Retain regions connected to the bottom of the image
      mask_connected ← RetainConnectedRegions(mask, connection="bottom")
      // Combine processed masks
      combined_mask ← MultiplyMasks(mask_connected, neighbor_mask)
  END FOR
  // Step 4: Analyze the mask to segment y-values
  y_coordinates ← IdentifyHighestYCoordinates(combined_mask)
  // Apply a changepoint algorithm to segment y-values
  segments ← SegmentYValues(y_coordinates)
  // Find the segment with the lowest median derivative
  best_segment ← SelectSegmentWithLowestDerivative(segments)
  // Create a new mask for the identified segment
  final_mask ← CreateMaskForSegment(combined_mask, segment=best_segment)
  // Return the final mask
  RETURN final_mask
END Algorithm

This algorithm has some failings and could be improved. A current failing of the algorithm is that it requires that the intersected facade be roughly the same dimensions as the original facade.

After processing our predicted mask with this algorithm, we are left with a mask which designates the two regions we want to simulate: photogrammetry noise and geometry obstruction. We can then pass this mask to a model to generate possible solutions for the missing regions.

Attaching historical data to facades data

In order to get historical data over the facades in Venice Cadastre 1808 was used. The data is a GeoDataFrame with polygons over the buildings in Venice and it contains historical information about the buildings such as ownership type. The polygons are from a hand drawn map of Venice and the buildings in Venice have also changed which has resulted in miss alignment of the buildings from the historical data with the current footprint of Venice. Thus, in order to attach the historical data to the facades a method for filtering out buildings and shifting the polygons has been developed.

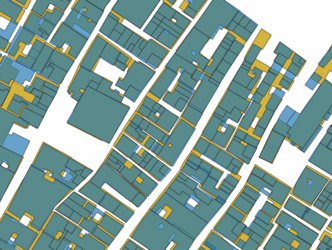
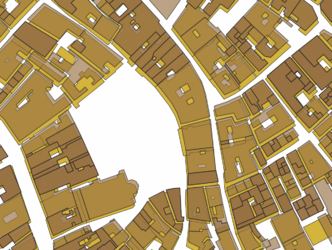
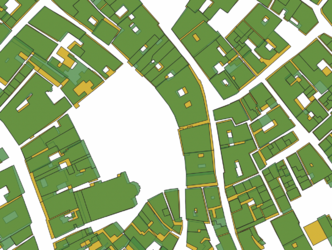
To align the datasets the current footprint of Venice the Edifici data was used mainly because of the difference in geometry between the cadastre buildings and the buildings of Venice today. Cadastre buildings are often smaller and simply attaching them to the closest facade would not provide good results because of the differences in geometry, to illustrate this and the miss alignment see figure 3.1, where cadastre buildings are shown in brown and Edifici buildings in yellow.

Figure 3.1: Edifici buildings are yellow and cadastre buildings are brown.

To better align the two maps, initial filtering of the data was done, since some Edifici buildings do not have any facade in the point cloud. These were filtered out to decrease the amount of data. Furthermore, there are duplicate entries of the same cadastre building in the dataset, this is not relevant when shifting the polygons thus these cases were also filtered out.

Two different metrics where used and evaluated for shifting the facades, percentage overlap and hausdorff distance. Percentage overlap between polygon A and B is defined as:

Percentage overlap(A, B) = (|A ∩ B|) / A

This was done for both Edifici and Cadastre polygons as there are cases where the Edifici polygon is smaller than the Cadastre polygon and vice versa. The Hausdorff distance is defined as the maximum distance between two polygons A and B. In this project, it was calculated by first joining all polygons overlapping an Edifici building and then computed using the hausdorff_distance method in GeoPandas.

The general approach for aligning and filtering the polygons can be outlined as follows:

1. Calculate metric

For every polygon in Edifici and Cadastre that overlap, calculate the metrics: percentage overlap and Hausdorff distance.

2. Filter buildings

Remove buildings that do not meet the specified criteria for percentage overlap or Hausdorff distance.

3. Identify easy cases

An easy case is a building that is well aligned in both maps. Easy cases were identified based on the metrics, either percentage overlap or Hausdorff distance.

4. Calculate offset between maps for easy cases

For every easy case, a vector between the centroids of the polygons in the two maps was calculated and stored.

5. Calculate the closest distance to an easy case and shift cadastre data

For every building in the cadastre dataset, the closest easy case was identified. The buildings in the Cadastre data were then all shifted by the vector in the closest easy case, multiplied by a learning rate smaller than 1.

6. Repeat until max iterations

For both methods, 25 iterations were used to shift the Cadastre polygons.

To compare the methods Jaccard index was used as the evaluation metric. The index distance is defined as: J(A, B) = 1 - (|A ∩ B|) / (|A ∪ B|) where:

• A and B are two building polygons.
• |A ∩ B| is the intersection area of A and B .
• |A ∪ B| is the size of their total area.

Grouping facades by attributes

After correctly attaching the cadastre data to our facades, we can then extract the following information:

1. Sestiere
2. Usage Type
3. Ownership Type

We combine this cultural data with the area of the facade, as given by the original dataset. Thus, we encode a specific facade in a multi-hot vector of 44 different attributes. These attributes are:

   'CANNAREGIO', 'CASTELLO', 'DORSODURO', 'LAGUNA', 'SAN MARCO', 'SAN POLO', 'SANTA CROCE', 
   'percentile_0%', 'percentile_10%', 'percentile_20%', 'percentile_30%', 'percentile_40%', 
   'percentile_50%', 'percentile_60%', 'percentile_70%', 'percentile_80%', 'percentile_90%', 
   'percentile_above_90', 
   'usage_', 'usage_ANDITO', 'usage_APPARTAMENTO', 'usage_BOTTEGA', 'usage_BOTTEGA, CASA', 
   'usage_BOTTEGA, CASA, CORTO', 'usage_BOTTEGA, CASA, CORTO, MAGAZZENO', 
   'usage_BOTTEGA, CASA, MAGAZZENO', 'usage_CASA', 'usage_CASA, CORTO', 
   'usage_CASA, CORTO, MAGAZZENO', 'usage_CASA, MAGAZZENO', 'usage_CHIESA', 'usage_CORTO',
   'usage_CORTO, MAGAZZENO', 'usage_CORTO, PALAZZO', 'usage_CORTO, SOTTOPORTICO', 
   'usage_MAGAZZENO', 'usage_MultipleUses', 'usage_PALAZZO', 
   'ownership_types_', 'ownership_types_AFFITTO', 'ownership_types_AFFITTO, COMMUNE',
   'ownership_types_AFFITTO, PROPRIO', 'ownership_types_COMMUNE', 'ownership_types_PROPRIO'

We use this cultural data in our implementation of a Conditional Variational-Autoencoder.

Model for Filling Holes

Based on our prior literature review, we found that many machine learning-based inpainting methods require manual definition of the regions to be filled. Fortunately, this step has already been completed. With the availability of masks for the holes, the process becomes significantly more straightforward. Our task is now more clearly defined as a specific inpainting problem.

At this stage, we aimed to test our images using various models, fine-tune those that meet our requirements and train some ones from scratch, then compare their performance differences. Majorly, our methods can be segmented into two types: data-variant and data-invariant methods.

Data-Invariant methods do not depend on our dataset. Analytical methods and extremely large pre-trained models fall into this subset. Data-Variant methods do depend on our dataset. We used two data-variant models trained from scratch on our validation dataset: Pix2Pix and a Conditional VAE-GAN.

Our basic algorithm to reconstruct a given facade was:

1. Identify the missing regions using the hole-identification algorithm.
2. Generate a solution given that facade
3. Combine the reconstruction and original facade using the identified hole mask.

Results

Attaching historical data to facades data

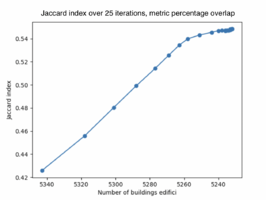
When shifting the facades for 25 iterations and using the metric percentage overlap the resulting average Jaccard index for the buildings is 0.548. The number of buildings kept after the final iteration is 5232 builings. See figure 4.1 for the results of the Jaccard index for each iteration.

• 

  Figure 4.1: Jaccard index when shifting the buildings for 25 iterations using metric percentage overlap.

• 

  Figure 4.2: Jaccard index when shifting the buildings for 25 iterations using metric Hausdorff distance.

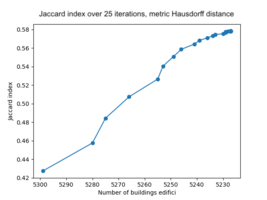
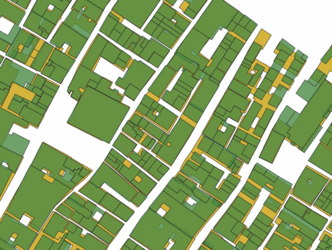
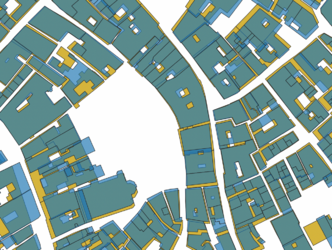
Using Hausdorff distance provides a higher resulting average Jaccard index of 0.578 after the final iteration and the number of buildings kept is 5227. See figure 4.2 for the results of the Jaccard index for each iteration. Filtering out buildings is done during the iterations and it is clear that this improves the overlap of the buildings. This is expected due to the difference in geometry of the Cadastre data and the Edifici data. Ideally, the performance when shifting the polygons would increase without buildings being removed, this would show that the shift improves the overlap of the buildings as well. This is less clear when looking at the performance of the Jaccard index. However, visually we can see the difference the shift makes, see figure 4.3 - 4.5. The yellow buildings in the figures are the Edifici buildings and the brown the cadastre buildings without being shifted. The blue buildings are the cadastre buildings shifted using Hausdorff distance and the green buildings are the cadastre buildings shifted using percentage overlap.

• 
• 
• 
• 

  Figure 4.3: Original Edifici and Cadastre geometries.

• 

  Figure 4.4: Filtered Edifici and shifted Cadastre geometries using percentage overlap as metric.

• 

  Figure 4.5: Filtered Edifici and shifted Cadastre geometries using Hausdorff distance as metric.

However, as can be seen in the bottom figure 4.4 sometimes overlaps are created between the polygons after shifting, this is dicussed further in the discussion and limitations.

Model for Filling Holes

Based on our prior literature review, we found that many machine learning-based inpainting methods require manual definition of the regions to be filled. The great thing is that this step has already been completed. With the availability of masks for the holes, the process becomes significantly more straightforward. Our task is now more clearly defined as a specific inpainting problem.

Data-Invariant Methods

While we do fine-tune these models, our fine-tune dataset is so inconsequential that we might as well describe those methods as data-invariant.

Stable Diffusion

We begin by using Stable Diffusion, a state-of-the-art text-to-image model that also supports inpainting. After conducting some initial tests, we present several examples of the generated images. As shown in Figure 4.3 and Figure 4.4, the pre-trained Stable Diffusion model struggles to fully capture the overall pattern of the image. The filled hole regions do not blend seamlessly with the existing areas; the generated regions and the original areas exhibit noticeably different styles.

• 

  Figure 4.3: Picture generated by using Stable Diffusion Inpainting.

• 

  Figure 4.4: Picture generated by using Stable Diffusion XL (SDXL) Inpainting.

Another issue lies with the prompts. We conducted some tests to explore this further. As shown in Figure 4.5 and Figure 4.6, we test the model with no prompts (`""`) and with prompts. While the generated images show differences between the two cases, they do not result in better outputs. Additionally, it remains unclear what prompts could be devised to enhance the model's performance for our specific task.

Also, there are certain special cases where Stable Diffusion fails to generate effective images, particularly when the hole regions are relatively large. In such instances, the generated images are often flagged as NSFW content and displayed entirely as black. See Figure 4.7.

• 

  Figure 4.5: Picture generated using Stable Diffusion Inpainting without prompt.

• 

  Figure 4.6: Picture generated using Stable Diffusion Inpainting with a prompt "venice facades, pixel, inpainting."

• 

  Figure 4.7: Generation failed due to "Potential NSFW content detected in one or more images. A black image was returned instead. Consider trying again with a different prompt and/or seed."

LaMa

After testing the Stable Diffusion model and encountering the aforementioned issues, we decide to shift our model strategy and identify a model more suitable for our task—automatically identifying patterns to fill missing regions without the need for prompts and demonstrating notable performance on low-resolution images. This leads us to the LaMa model.

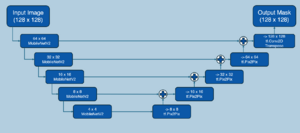
LaMa is a model designed for large-mask inpainting, introduced by Roman Suvorov et al. in 2021. It features a ResNet-inspired feed-forward inpainting network, incorporating fast Fourier convolution (FFC), a multi-component loss combining adversarial and high receptive field perceptual losses, and a training-time procedure for large mask generation. See Figure 4.8 for its structure.

Figure 4.8: Architecture of the LaMa model. Source: https://arxiv.org/pdf/2109.07161.pdf

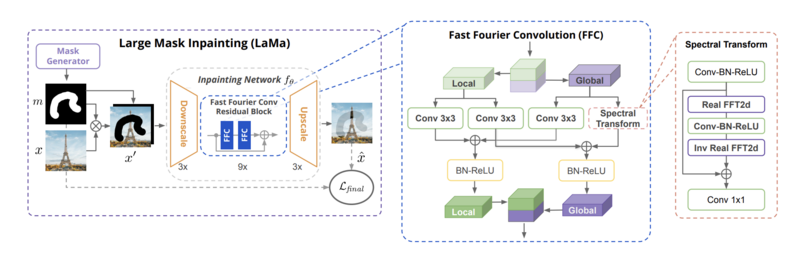
LaMa offers several key advantages over Stable Diffusion, making it particularly well-suited for our inpainting tasks:

1. LaMa is lightweight and runs inference quickly, even on CPUs, whereas Stable Diffusion is computationally heavy and requires powerful GPUs.

2. Stable Diffusion relies on prompts, which can make its performance inconsistent and less predictable for our specific needs. While LaMa is deterministic and consistently produces the same output for the same input.

3. LaMa excels at completing repetitive or structured patterns. Stable Diffusion focuses on generating creative, diverse outputs rather than maintaining structured consistency.

Also, from our previous experiments, even though Stable Diffusion has more powerful capabilities, the low resolution of our images provides limited information for the model to learn from. As a result, Stable Diffusion fails to capture the patterns we need. This suggests that Stable Diffusion may not be well-suited for low-resolution images.

The initial idea is to either train the model from scratch or fine-tune a pre-trained model with the best performance. However, according to an article , training from scratch does not show any significant improvement. Also, our available dataset for training is relatively small, so we decided to proceed with fine-tuning. There are two versions of LaMa we can work with: one is the original model, and the other includes feature refinement proposed in another paper . We first conduct tests using both the original model and the feature-refinement-enhanced version to evaluate whether our images would perform better with the additional refinement.

See Figure 4.9-4.12, we find that the feature-refinement-enhanced model did not demonstrate stronger inpainting capabilities on our dataset. Across several test images, the results are indistinguishable from those produced by the original model. This might be partially due to the fact that feature refinement is tailored for high-resolution images, as stated in the original paper: "In this paper, we address the problem of degradation in inpainting quality of neural networks operating at high resolutions...To get the best of both worlds, we optimize the intermediate featuremaps of a network by minimizing a multiscale consistency loss at inference. This runtime optimization improves the inpainting results and establishes a new state-of-the-art for high resolution inpainting." Clearly, our images are of very low resolution, therefore, we decide to proceed with the original model for subsequent tasks.

• 

  Figure 4.9: Picture example 1 generated by LaMa without feature refinement.

• 

  Figure 4.10: Picture example 1 generated by LaMa with feature refinement.

• 

  Figure 4.11: Picture example 2 generated by LaMa without feature refinement.

• 

  Figure 4.12: Picture example 2 generated by LaMa with feature refinement.

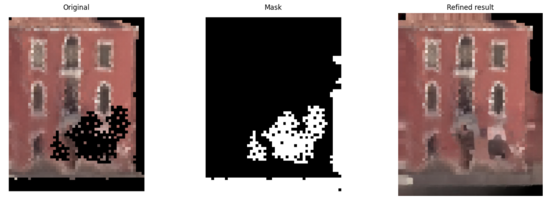
Next, to fine-tune our model, we need a dataset tailored to its requirements, specifically images with high completeness to provide sufficient training information. However, our original dataset primarily consists of images with holes and lacked corresponding ground truth data. Fortunately, during the earlier hole identification phase, we create a validation set containing relatively complete facades and masks. Unlike the official implementation, where the model automatically generates masks of varying thicknesses (thin, medium, thick), we design a custom input structure in which each original image is paired with six corresponding masks, each containing artificial holes created by us to represent different hole configurations.

Compared to Stable Diffusion, we do find that Lama demonstrates strong pattern recognition capabilities in image processing, even for low-resolution images. The filled gaps can blend more naturally into the original images. See Figure 4.13 and 4.14. However, we also observe some limitations of LaMa. Even after fine-tuning, our model still struggles to handle cases with larger holes effectively. It does make progress in filling larger holes, especially around the outer edges of the missing regions. However, the interior of the holes still remains incomplete and unfilled. We will elaborate more details in the "discussion of limitations" part.

• 

  Figure 4.13: Picture example 1 generated after fune-tuning LaMa.

• 

  Figure 4.14: Picture example 2 generated after fune-tuning LaMa.

Kriging

We also used the analytical method of kriging to generate solutions. We used PyKrieg's implementation.

Data-Variant Methods

Pix2Pix + Perceptual Loss

Although this was not the first method attempted, Pix2Pix is the simpler of the two data-variant methods. This method adapts the model Pix2Pix as described by Isola et. al. This method adapts the UNet "skip-connection" architecture to the Encoder-Decoder framework for image-to-image translation. One of the example uses of this model in the paper was mapping building labels to facades, so we were sure that this would generalize well to facade reconstruction.

We implemented the model as described by the paper and in a TensorFlow tutorial . In a novel addition to our model, we also added a perceptual loss as described by Johnson et. al. This addition of the perceptual loss improved our model's ability to learn fine-grained features and to avoid generating blurry reconstructions.

In implementing Pix2Pix, we also trained a patch-specific discriminator.

We trained our model on the artificially-generated holes of our validation dataset. We trained our model for about 50,000 steps. Our model still has a long way to go, and has yet to converge. However, it is already producing useful results.

• 

  Pix2Pix Architecture from Isola et. al.

• 
• 
• 
• 
• 
• 

Conditional Variational Autoencoder with a Discriminator

We also implemented a Conditional VAE-GAN. VAE's were originally described by Kingma and Welling. We based our implementation off of the VAE described by the TensorFlow tutorial for VAEs. However, if we want to reconstruct images using this architecture, we need to adapt it to take in a conditional input for reconstruction. We followed the work of Sohn et. al. in creating a Conditional VAE. To adapt this model for our use case characterized by fine-grained features, we also implemented and added a perceptual loss (the same as in the Pix2Pix model) and a discriminator.

• 
• 
• 

Quality assessment and discussion of limitations

Attaching historical data to facades data

To assess the quality of the shift of the building the Jaccard Index was used. Furthermore, after shifting the buildings the results where analysed visually using QGIS. By doing this overlaps between shifted buildings where identified. Therefore, the number of overlaps between buildings were also calculated. Different methods for decreasing the number of overlapping buildings was tried such as decreasing the shift rate or "learning rate". Other approaches could be to only shift buildings within a certain radius of an easy case or to prevent shifts causing overlaps. However, doing this might also cause some buildings to never shift. Another way could be to identify more easy cases. This could be done by decreasing the hausdorff distance or percentage overlap. Another metric such as average Hausdorff distance could also be used to identify easy cases.

Another approach that could be tried to potentially increase the performance of the shift is to calculate the vector between the overlapping polygons attempt to do a shift and if the shift results in a significant improvement of the metric to use it as a easy case.

Filling holes with LaMa

Even after fine-tuning, we find that LaMa has limitations in filling large hole areas. We think one possible reason is that, for the internal part of the holes, the model mistakenly assumes this area should be filled with adjacent parts, which are also black and need to be filled. One approach we try is to feed the filled picture back into the model, recalculate the mask, and input it into LaMa again to see if the unfilled parts can be addressed. However, most pictures show no improvement, see Figure 5.1. In the few cases where there is improvement, it is limited to small holes, See Figure 5.2, only the left small part is filled after the second attempt, however, with no noticeable progress in larger holes.

• 

  Figure 5.1: Use LaMa to fill holes twice example 1.

• 

  Figure 5.2: Use LaMa to fill holes twice example 2.

Appendix

Github: https://github.com/ccpfoye/fdh_project